
 .
. ,
, )
) .
.  ,因各炮射击的结果是相互独立的,所以
,因各炮射击的结果是相互独立的,所以

 .
.  ,即
,即  ,
,  ,
, 

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:不详 题型:填空题
 表达式中的
表达式中的 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数 表达式中的
表达式中的 则一次函数
则一次函数 的图象经过二、三、四象限的概率是 .
的图象经过二、三、四象限的概率是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
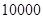 次还能继续使用的概率是
次还能继续使用的概率是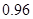 ,开关了
,开关了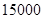 次后还能继续使用的概率是
次后还能继续使用的概率是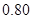 ,则已经开关了
,则已经开关了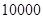 次的电视机显像管还能继续使用到
次的电视机显像管还能继续使用到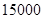 次的概率是 。
次的概率是 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,
, ,
, ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.  的概率及
的概率及 的数学期望
的数学期望 ;
;  .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
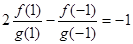 ,在有穷数列{
,在有穷数列{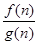 }(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{
}(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{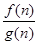 }前k项和大于
}前k项和大于 的概率是( )
的概率是( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com