
【题目】已知函数f(x)=-x3+x2+b,g(x)=aln x.
(1)若f(x)在![]() 上的最大值为
上的最大值为![]() ,求实数b的值;
,求实数b的值;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围.
【答案】(1)b=0; (2)a≤-1.
【解析】
(1)由f(x)=﹣x3+x2+b,得f′(x)=﹣3x2+2x=﹣x(3x﹣2),令f′(x)=0,得x=0或x=![]() .由此列表讨论能求出b=0.
.由此列表讨论能求出b=0.
(2)由g(x)≥﹣x2+(a+2)x,得(x﹣lnx)a≤x2﹣2x.由已知得a≤(![]() )min.由此利用构造法和导数性质能求出a≤﹣1.
)min.由此利用构造法和导数性质能求出a≤﹣1.
(1)由f(x)=-x3+x2+b,得f′(x)=-3x2+2x=-x(3x-2),令f′(x)=0,得x=0或x=![]() .列表如下:
.列表如下:
x | - |
| 0 |
|
|
|
f′(x) | - | 0 | + | 0 | - | |
f(x) | f | ↘ | 极小值 | ↗ | 极大值 | ↘ |
由f![]() =
=![]() +b,f
+b,f![]() =
=![]() +b,∴f
+b,∴f![]() >f
>f![]() ,即函数f(x)在
,即函数f(x)在![]() 上的最大值为f
上的最大值为f![]() =
=![]() +b=
+b=![]() ,∴b=0.
,∴b=0.
(2)由g(x)≥-x2+![]() x,得
x,得![]() a≤x2-2x.∵x∈[1,e],∴ln x≤1≤x,且等号不能同时成立,∴ln x<x,即x-ln x>0,∴a≤
a≤x2-2x.∵x∈[1,e],∴ln x≤1≤x,且等号不能同时成立,∴ln x<x,即x-ln x>0,∴a≤![]() 恒成立,即a≤
恒成立,即a≤![]() .令t(x)=
.令t(x)=![]() ,x∈[1,e],求导得,t′(x)=
,x∈[1,e],求导得,t′(x)=![]() ,当x∈[1,e]时,x-1≥0,ln x≤1,x+2(1-ln x)>0,从而t′(x)≥0,∴t(x)在[1,e]上为增函数,∴t(x)min=t(1)=-1,∴a≤-1.
,当x∈[1,e]时,x-1≥0,ln x≤1,x+2(1-ln x)>0,从而t′(x)≥0,∴t(x)在[1,e]上为增函数,∴t(x)min=t(1)=-1,∴a≤-1.


科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
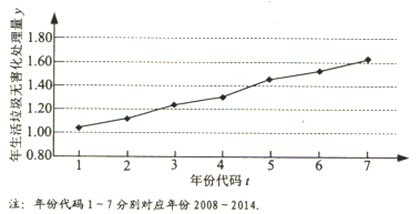
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;
单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an} 为等比数列,等差数列{bn} 的前n 项和为Sn (n∈N* ),且满足:S13=208,S9﹣S7=41,a1=b2 , a3=b3 .
(1)求数列{an},{bn} 的通项公式;
(2)设Tn=a1b1+a2b2+…+anbn (n∈N* ),求Tn;
(3)设cn= ![]() ,问是否存在正整数m,使得cmcm+1cm+2+8=3(cm+cm+1+cm+2).
,问是否存在正整数m,使得cmcm+1cm+2+8=3(cm+cm+1+cm+2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1 , x2∈[0,2]且x1≠x2时,都有 ![]() <0,给出下列四个命题:
<0,给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为增函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ax2+bx,(a,b∈R).
(1)设a=1,f(x)在x=1处的切线过点(2,6),求b的值;
(2)设b=a2+2,求函数f(x)在区间[1,4]上的最大值;
(3)定义:一般的,设函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称x0为函数g(x)的不动点.设a>0,试问当函数f(x)有两个不同的不动点时,这两个不动点能否同时也是函数f(x)的极值点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com