
分析 (Ⅰ)当a=0时,$f(x)=2lnx+\frac{1}{x}$,定义域为(0,+∞),求出f(x)的导函数.判断导函数的符号,推出导函数的单调性,然后求解极值、
(Ⅱ)当a<0时,$f(x)=(2-a)lnx+\frac{1}{x}+2ax$的定义域为(0,+∞),求出f(x)的导函数,由f′(x)=0得极值点,通过(1)当-2<a<0时,(2)当a=-2时,(3)当a<-2时,分别求解函数的单调区间即可.
解答 解:(Ⅰ)当a=0时,$f(x)=2lnx+\frac{1}{x}$,定义域为(0,+∞),
f(x)的导函数${f^'}(x)=\frac{2}{x}-\frac{1}{x^2}=\frac{2x-1}{x^2}$.
当$0<x<\frac{1}{2}$时,f′(x)<0,f(x)在$(0,\frac{1}{2})$上是减函数;
当$x>\frac{1}{2}$时,f′(x)>0,f(x)在$(\frac{1}{2},+∞)$上是增函数.
∴当$x=\frac{1}{2}$时,f(x)取得极小值为$f(\frac{1}{2})=2-2ln2$,无极大值.
(Ⅱ)当a<0时,$f(x)=(2-a)lnx+\frac{1}{x}+2ax$的定义域为(0,+∞),f(x)的导函数为${f^'}(x)=\frac{2-a}{x}-\frac{1}{x^2}+2a=\frac{{2a{x^2}+(2-a)x-1}}{x^2}=\frac{(2x-1)(ax+1)}{x^2}$.
由f′(x)=0得${x_1}=\frac{1}{2}>0$,${x_2}=-\frac{1}{a}>0$,${x_1}-{x_2}=\frac{1}{2}-(-\frac{1}{a})=\frac{a+2}{2a}$.
(1)当-2<a<0时,f(x)在$(0,\frac{1}{2})$上是减函数,在$(\frac{1}{2},-\frac{1}{a})$上是增函数,在$(-\frac{1}{a},+∞)$上是减函数;
(2)当a=-2时,f(x)在(0,+∞)上是减函数;
(3)当a<-2时,f(x)在$(0,-\frac{1}{a})$上是减函数,在$(-\frac{1}{a},\frac{1}{2})$上是增函数,
在$(\frac{1}{2},+∞)$上是减函数.
综上所述,
当a<-2时,f(x)在$(0,-\frac{1}{a}),(\frac{1}{2},+∞)$上是减函数,在$(-\frac{1}{a},\frac{1}{2})$上是增函数;
当a=-2时,f(x)在(0,+∞)上是减函数;
当-2<a<0时,f(x)在$(0,\frac{1}{2}),(-\frac{1}{a},+∞)$上是减函数,在$(\frac{1}{2},-\frac{1}{a})$上是增函数.
(Ⅲ)由(Ⅱ)知,当a∈(-∞,-2)时,f(x)在[1,3]上是减函数.
∴$|f({x_1})-f({x_2})|≤f(1)-f(3)=\frac{2}{3}-4a+(a-2)ln3$.
∵对于任意的x1,x2∈[1,3],a∈(-∞,-2)都有|f(x1)-f(x2)|<(m+ln3)a-2ln3,
∴$\frac{2}{3}-4a+(a-2)ln3<(m+ln3)a-2ln3$对任意a<-2恒成立,
∴$m<-4+\frac{2}{3a}$对任意a<-2恒成立.
当a<-2时,$-\frac{13}{3}<-4+\frac{2}{3a}<-4$,∴$m≤-\frac{13}{3}$.
∴实数m的取值范围为$(-∞,-\frac{13}{3}]$.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性的判断以及考查分类讨论思想转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
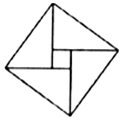 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
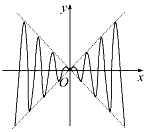 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )| A. | x2sinx | B. | xsinx | C. | x2cosx | D. | xcosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com