
【题目】如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
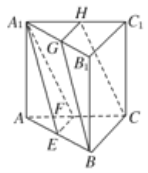
求证:(1)GH∥面ABC
(2)平面EFA1∥平面BCHG.
【答案】(1)见解析(2)见解析
【解析】
(1) 根据三角形中位线定理以及三棱柱的性质可推导出![]() ,由线面平行的判定定理能证明
,由线面平行的判定定理能证明![]() 面
面![]() ;(2)由三角形中位线定理推导出
;(2)由三角形中位线定理推导出![]() ,由平行四边形的性质可得
,由平行四边形的性质可得![]() ,从而可证明平面
,从而可证明平面![]() 平面
平面![]() .
.
(1)∵在三棱柱ABCA1B1C1中,
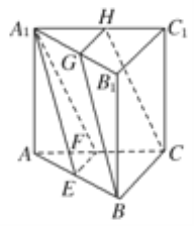
E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
∴GH∥B1C1∥BC,
∵GH平面ABC,BC平面ABC,
∴GH∥面ABC.
(2)∵在三棱柱ABCA1B1C1中,
E,F,G,H分别是AB,AC,A1B1,A1C1的中点,
∴EF∥BC,A1G![]() BE,
BE,
∴四边形BGA1E是平行四边形,∴A1E∥BG,
∵A1E∩EF=E,BG∩BC=B,
A1E,EF平面EFA1,BG,BC平面BCHG,
∴平面EFA1∥平面BCHG.


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(α>b>0)的右焦点到直线x﹣y+3
=1(α>b>0)的右焦点到直线x﹣y+3 ![]() =0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为
=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为 ![]() .
.
(1)求椭圆C的方程;
(2)在x轴上是否存在点Q,使得过Q的直线与椭圆C交于A、B两点,且满足 ![]() +
+ ![]() 为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,其中e是自然对数的底数.
是R上的偶函数,其中e是自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)探究函数![]() 在
在![]() 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若函数![]() 有零点,求实数m的取值范围.
有零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图像与
的图像与![]() 轴的交点为
轴的交点为![]() ,在
,在![]() 轴右侧的第一个最高点和第一个与
轴右侧的第一个最高点和第一个与![]() 轴交点分别为
轴交点分别为![]()
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 图像上所有点的横坐标变为原来的
图像上所有点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图像沿
倍(纵坐标不变),再将所得图像沿![]() 轴正方向平移
轴正方向平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像,求
的图像,求![]() 的解析式;
的解析式;
(3)在(2)的条件下求函数![]() 在
在![]() 上的值域。
上的值域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com