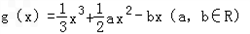练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设函数，在其图象上一点P（x，y）处的切线的斜率记为f（x）．
    （1）若方程f（x）=0有两个实根分别为﹣2和4，求f（x）的表达式；
    （2）若g（x）在区间[﹣1，3]上是单调递减函数，求a2+b2的最小值．
    解：（1）根据导数的几何意义知f（x）=g'（x）=x2+ax﹣b
    由已知﹣2、4是方程x2+ax﹣b=0的两个实数
    由韦达定理，∴，
    f（x）=x2﹣2x﹣8
    （2）g（x）在区间[﹣1，3]上是单调减函数，
    所以在[﹣1，3]区间上恒有f（x）=g'（x）=x2+ax﹣b≤0，
    即f（x）=x2+ax﹣b≤0在[﹣1，3]恒成立
    这只需满足即可，也即
    而a2+b2可视为平面区域内的点到原点距离的平方，
    其中点（﹣2，3）距离原点最近，所以当时，a2+b2有最小值13．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2011•聊城一模）已知函数f(x)=sin(2ωx-
    π
    6
    )-4sin2ωx+a，(ω＞0)    ，其图象的相邻两个最高点之间的距离为π，
    （1） 求函数f（x）的单调递增区间；
    （2） 设函数f（x）在区间[0，
    π
    2
    ]    上的最小值为-
    3
    2
    ，求函数f（x），（x∈R）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•枣庄一模）已知函数f（x）=
    1
    2
    x2-2x，g(x)=loga    x（a＞0，且a≠1），其中a为常数，如果h（x）=f（x）+g（x）在其定义域上是增函数，且h'（x）存在零点（h'（x）为h（x）的导函数）．
    （I）求a的值；
    （Ⅱ）设A（m，g（m）），B（n，g（n））（m＜n）是函数y=g（x）的图象上两点，g'（x0）=
    g(n)-g(m)
    n-m
    （g'（x）为g（x）的导函数），证明：m＜x0＜n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•眉山一模）设函数f（x）对其定义域内的任意实数x1与x2都有f(
    x1+x2
    2
    )≥
    f(x1)+f(x2)
    2
    ，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有f(
    x1+x2+…+xn
    n
    )≥
    f(x1)+f(x2)+…+f(xn)
    n
    （当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
    ①f（x）=lnx（x＞0）是上凸函数；
    ②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
    ③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且
    AC
    =λ
    CB
    ，则f(
    x1+λx2
    1+λ
    )≥
    f(x1)+λf(x2)
    1+λ
    ；
    ④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是
    3
    		3
    2
    ．
    其中，正确命题的序号是
    ①③④
    ①③④
    （写出所有你认为正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数g(x)= (a，b∈R)，在其图象上一点P(x,y)处的切线的斜率记为f(x)．

       （1）若方程f(x)=0有两个实根分别为一2和4，求f(x)的表达式；

       （2）若g(x)在区间[一1，3]上是单调递减函数，求a2+b2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)的定义域为D，若存在x0∈D，使得y0=f(x0)=x0，则称以(x0,y0)为坐标的点为函数图象上的不动点.

    (1)若函数f(x)=的图象上有两个关于原点对称的不动点，求a、b满足的条件;

    (2)在(1)的条件下，若a=8，记函数f(x)图象上的两个不动点分别为A、A′，P为函数f(x)的图象上的另一点，且其纵坐标yP＞3，求点P到直线AA′距离的最小值及取得最小值时点P的坐标.

    (3)命题“若定义在R上的奇函数f(x)的图象上存在有限个不动点，则不动点有奇数个”是否正确？若正确，试给予证明，并举出一例；若不正确，试举一反例说明.

    查看答案和解析>>

    同步练习册答案