
分析 (1)由题设知a=$\sqrt{2}$,所以$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,椭圆经过点P(1,$\frac{\sqrt{2}}{2}$),代入可得b=1,a=$\sqrt{2}$,由此可知所求椭圆方程;
(2)设AM、AN的方程,代入椭圆方程,求出M,N的坐标,进而可得MN恒过定点(0,0).
解答 解:(1)∵椭圆两焦点与短轴的一个端点构成等腰直角三角形.
∴a=$\sqrt{2}$b,∴$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
又∵椭圆经过点P(1,$\frac{\sqrt{2}}{2}$),代入可得b=1,
∴a=$\sqrt{2}$,故所求椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)直线MN过定点(0,0),
证明:设过椭圆右顶点A($\sqrt{2}$,0)的直线l1的方程为y=k1(x-$\sqrt{2}$),
代入椭圆方程,消去y,得(1+2k12)x2-4$\sqrt{2}$k12x+4k12-2=0,
则xM=$\frac{2\sqrt{2}{{k}_{1}}^{2}-\sqrt{2}}{1+2{{k}_{1}}^{2}}$,yM=k1xM-$\sqrt{2}$k1=-$\frac{2\sqrt{2}{k}_{1}}{1+2{{k}_{1}}^{2}}$,
则M($\frac{2\sqrt{2}{{k}_{1}}^{2}-\sqrt{2}}{1+2{{k}_{1}}^{2}}$,-$\frac{2\sqrt{2}{k}_{1}}{1+2{{k}_{1}}^{2}}$),
由于l2的方程为y=k2(x-$\sqrt{2}$),且k1•k2=-$\frac{1}{2}$,
代入椭圆方程,则将上面的k1换成-$\frac{1}{2{k}_{1}}$,
有N(-$\frac{2\sqrt{2}{{k}_{1}}^{2}-\sqrt{2}}{1+2{{k}_{1}}^{2}}$,$\frac{2\sqrt{2}{k}_{1}}{1+2{{k}_{1}}^{2}}$),
则有M,N两点关于原点对称,
连接MN,必过原点(0,0).
故直线MN恒过定点(0,0).
点评 本题考查椭圆的性质和综合运用,计算量较大,解题时要认真审题,仔细求解.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | |PP1|=|AA1|+|BB1| | B. | |PP1|=$\frac{1}{2}$|AB| | C. | |PP1|>$\frac{1}{2}$|AB| | D. | |PP1|$<\frac{1}{2}$|AB| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 当天处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 当天闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
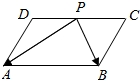 如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.
如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com