
分析 (1)记“第i次取到红球”为Ai(i=1,2),则先后取一球,恰好摸到一个红球和一个白球可表示为${A_1}\overline{A_2}$+$\overline{A_1}{A_2}$,由此能求出恰好取到1个红球,1个白球的概率.
(2)采用放回抽样,每次取到红球的概率$P=\frac{2}{6}=\frac{1}{3}$,连续取5次,可看作5次独立重复试验,由此能求出恰有两次取到红球的概率.
解答 解:(1)记“第i次取到红球”为Ai(i=1,2),
则先后取一球,恰好摸到一个红球和一个白球可表示为${A_1}\overline{A_2}$+$\overline{A_1}{A_2}$,
其概率为P(${A_1}\overline{A_2}$+$\overline{A_1}{A_2}$)=P(${A_1}\overline{A_2}$)+P($\overline{A_1}{A_2}$)=$\frac{2}{6}×\frac{4}{5}+\frac{4}{6}×\frac{2}{5}=\frac{8}{15}$,
∴恰好取到1个红球,1个白球的概率为$\frac{8}{15}$…(6分)
(2)采用放回抽样,每次取到红球的概率$P=\frac{2}{6}=\frac{1}{3}$.
连续取5次,可看作5次独立重复试验,…(9分)
∴恰有两次取到红球的概率为${P_5}(2)=C_5^2×{(\frac{1}{3})^2}×{(\frac{2}{3})^3}=\frac{80}{243}$.…(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式、互斥事件概率加法公式、n次独立重复试验概率计算公式的合理运用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
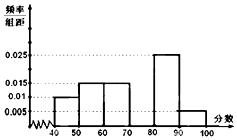 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
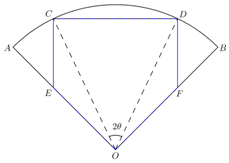 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
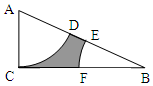 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
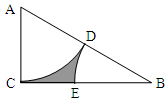 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | 1-$\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | 1-$\frac{π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{27}$ | D. | $\frac{12}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com