
���� ��1���ȷֱ�۲����������ĸ���Ϊ��1��1+4��1+4+8�������������f��5����
��2���ܽ�һ���ԵĹ��ɣ���֪f��n+1��-f��n��=4n�����õ��ӷ�������f��n���ı���ʽ��
��3������ͨ���ص㣬���������ͣ�������еĵ����Լ��ɵ�֤��
��� �⣺��1��f��1��=1��f��2��=1+4=5��
f��3��=1+4+8=13��f��4��=1+4+8+12=25��
f��5��=1+4+8+12+16=41��f��6��=1+4+8+12+16+20=61��
��2����f��2��-f��1��=4=4��1��
f��3��-f��2��=8=4��2��
f��4��-f��3��=12=4��3��
f��5��-f��4��=16=4��4��
����ʽ���ɵó�f��n+1��-f��n��=4n��
��f��n��-f��n-1��=4��n-1����
f��n-1��-f��n-2��=4•��n-2����
f��n-2��-f��n-3��=4•��n-3����
��
f��2��-f��1��=4��1��
��f��n��-f��1��=4[��n-1��+��n-2��+��+2+1]
=2��n-1��•n��
��f��n��=2n2-2n+1��
��3��֤������n��2ʱ��$\frac{1}{f��n��-1}$=$\frac{1}{2{n}^{2}-2n+1-1}$=$\frac{1}{2}$��$\frac{1}{n-1}$-$\frac{1}{n}$����
��$\frac{1}{f��1��}$+$\frac{1}{f��2��-1}$+$\frac{1}{f��3��-1}$+��+$\frac{1}{f��n��-1}$=1+$\frac{1}{2}$��1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+��+$\frac{1}{n-1}$-$\frac{1}{n}$��
=1+$\frac{1}{2}$��1-$\frac{1}{n}$��=$\frac{3}{2}$-$\frac{1}{2n}$��
n=1ʱ����ʽҲ������
����g��n��=$\frac{3}{2}$-$\frac{1}{2n}$Ϊ�������У�
����g��n����g��1��=1��
��g��n����$\frac{3}{2}$��
��1��$\frac{1}{f��1��}$+$\frac{1}{f��2��-1}$+$\frac{1}{f��3��-1}$+��+$\frac{1}{f��n��-1}$��$\frac{3}{2}$������
���� ������Ҫ������������������˼·���ȷ������壬�۲죬�ܽ���������ϵ���õ�һ���ԵĽ��ۣ�ͬʱ��������������еĺͣ������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��1�� | B�� | ��1��2�� | C�� | ��-1��-2�� | D�� | ��2��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8733 | B�� | 8710 | C�� | 8726 | D�� | 8717 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
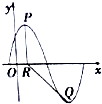 ��֪����f��x��=Asin��$\frac{��}{3}x$+�գ�����A��0��0���գ�$\frac{��}{2}$����y=f��x���IJ���ͼ����ͼ��ʾ��P��Q�ֱ�Ϊ��ͼ�������ڵ���ߵ����͵㣬��P��x���ϵ���ӰΪR��1��0����cos��PRQ=-$\frac{4}{5}$��
��֪����f��x��=Asin��$\frac{��}{3}x$+�գ�����A��0��0���գ�$\frac{��}{2}$����y=f��x���IJ���ͼ����ͼ��ʾ��P��Q�ֱ�Ϊ��ͼ�������ڵ���ߵ����͵㣬��P��x���ϵ���ӰΪR��1��0����cos��PRQ=-$\frac{4}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
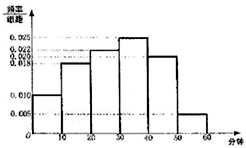 ���Ӵ�ý��˾Ϊ���˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��
���Ӵ�ý��˾Ϊ���˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ�� | �������� | ������ | �ϼ� | |
| �� | |||
| Ů | |||
| �ϼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1-3ln2�� | B�� | ��1��3ln2-1�� | C�� | ��1-3ln2��1�� | D�� | ��1��+�ޣ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com