
【题目】如图,已知矩形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,现沿着
的中点,现沿着![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() .
.
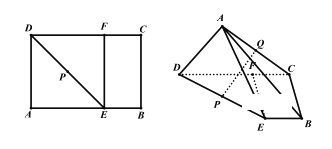
(1)![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() .
.
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,得
,得![]() ,利用线面平行的判定定理得
,利用线面平行的判定定理得![]() 平面
平面![]() ;∵
;∵![]() 是
是![]() 的中位线,∴
的中位线,∴![]() ,再利用线面平行的判定定理得
,再利用线面平行的判定定理得![]() 平面
平面![]() ,且
,且![]() ,即可证得;
,即可证得;
(2)连接![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,根据余弦定理可求得
,根据余弦定理可求得![]() ,同理:
,同理:![]() ;∵平面
;∵平面![]() 平面
平面![]() ,得在
,得在![]() ,∴
,∴![]() ,进而得
,进而得![]() ,利用
,利用![]() ,即可求出点
,即可求出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,易证
,易证![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴
∴![]() 平面
平面![]() .
.
∵![]() 是
是![]() 的中位线,∴
的中位线,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() ,∵
,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)连接![]() ,
,![]() ,
,![]() ,∵
,∵![]() ,且点
,且点![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,且
,且![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,根据余弦定理可求得
,根据余弦定理可求得![]() ,
,
所以![]() .同理:在
.同理:在![]() 中,
中,![]() ,可求得
,可求得![]() ;
;
在![]() ,∴
,∴![]() ,
,
同理可求得![]() ,∴
,∴![]() 为等腰三角形,
为等腰三角形,![]() ,∴
,∴![]() ,
,
三棱锥![]() 的高为
的高为![]() ,
,![]() ,
,
设点![]() 到平面
到平面![]() 距离为
距离为![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.



科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中a为实数.
,其中a为实数.
(1)当a=-1时,求函数y=f(x)的零点;
(2)若f(x)在(-2,2)上为增函数,求实数a的取值范围;
(3)对于给定的实数a,若存在两个不相等的实数根![]() ,
,![]() ,(
,(![]() <
<![]() 且
且![]() ≠0)使得f(
≠0)使得f(![]() )=f(
)=f(![]() ),求
),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的导函数
的导函数![]() 的图象如图所示,则以下关于函数
的图象如图所示,则以下关于函数![]() 的判断:
的判断:
①在区间![]() 内单调递增;
内单调递增;
②在区间![]() 内单调递减;
内单调递减;
③在区间![]() 内单调递增;
内单调递增;
④![]() 是极小值点;
是极小值点;
⑤![]() 是极大值点.
是极大值点.
其中正确的是( )
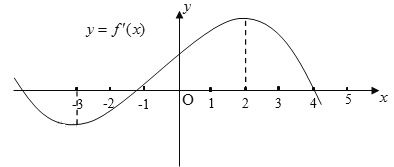
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】缴纳个人所得税是收入达到缴纳标准的公民应尽的义务.
①个人所得税率是个人所得税额与应纳税收入额之间的比例;
②应纳税收入额=月度收入-起征点金额-专项扣除金额(三险一金等);
③2018年8月31日,第十三届全国人民代表大会常务委员会第五次会议《关于修改中华人民共和国个人所得税法的决定》,将个税免征额(起征点金额)由3500元提高到5000元.下面两张表格分别是2012年和2018年的个人所得税税率表:
2012年1月1日实行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过1500元的部分 | 3 | 0 |
二 | 超过1500元至4500元的部分 | 10 | 105 |
三 | 超过4500元至9000元的部分 | 20 | 555 |
四 | 超过9000元至35000元的部分 | 25 | 1005 |
五 | 超过35000元至55000元的部分 | 30 | 2755 |
六 | 超过55000元至80000元的部分 | 35 | 5505 |
七 | 超过80000元的部分 | 45 | 13505 |
2018年10月1日试行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过3000元的部分 | 3 | 0 |
二 | 超过3000元至12000元的部分 | 10 | 210 |
三 | 超过12000元至25000元的部分 | 20 | 1410 |
四 | 超过25000元至35000元的部分 | 25 | 2660 |
五 | 超过35000元至55000元的部分 | 30 | 4410 |
六 | 超过55000元至80000元的部分 | 35 | 7160 |
七 | 超过80000元的部分 | 45 | 15160 |
(1)何老师每月工资收入均为13404元,专项扣除金额3710元,请问何老师10月份应缴纳多少元个人所得税?若与9月份相比,何老师增加收入多少元?
(2)对于财务人员来说,他们计算个人所得税的方法如下:应纳个人所得税税额=应纳税收入额×适用税率-速算扣除数,请解释这种计算方法的依据?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com