Question

已知函数f(x)的导函数为f ′(x)，且对任意x＞0，都有f ′(x)＞．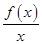

（Ⅰ）判断函数F(x)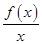＝在(0，＋∞)上的单调性；

（Ⅱ）设x₁，x₂∈(0，＋∞)，证明：f(x₁)＋f(x₂)＜f(x₁＋x₂)；

（Ⅲ）请将（Ⅱ）中的结论推广到一般形式，并证明你所推广的结论．

 

Answer 1

【答案】

（Ⅰ）F(x)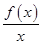＝在(0，＋∞)上是增函数；（Ⅱ）f(x₁)＋f(x₂)＜f(x₁＋x₂)；（Ⅲ）f(x₁)＋f(x₂)＋…＋f(x_n)＜f(x₁＋x₂＋…＋x_n).

【解析】

试题分析：（Ⅰ）判断F(x)的单调性，则需对F(x)求导，得F′(x)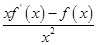＝，∵f ′(x)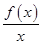＞，x＞0，则xf ′(x)－f(x)＞0，即F′(x)＞0，F(x)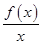＝在(0，＋∞)上是增函数.（Ⅱ）要证明f(x₁)＋f(x₂)＜f(x₁＋x₂)，可以从第（Ⅰ）的结论入手，∵x₁＞0，x₂＞0，∴0＜x₁＜x₁＋x₂，F(x)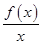＝在(0，＋∞)上是增函数，则F(x₁)＜F(x₁＋x₂)，即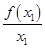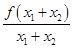＜，而x₁＞0，所以f(x₁)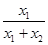＜f(x₁＋x₂)，同理f(x₂)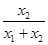＜f(x₁＋x₂)，两式相加，得f(x₁)＋f(x₂)＜f(x₁＋x₂)，得证.（Ⅲ）（Ⅱ）中结论的推广形式为：设x₁，x₂，…，x_n∈(0，＋∞)，其中n≥2，则f(x₁)＋f(x₂)＋…＋f(x_n)＜f(x₁＋x₂＋…＋x_n)．证明的方法同（Ⅱ）的证明，∵x₁＞0，x₂＞0，…，x_n＞0，∴0＜x₁＜x₁＋x₂＋…＋x_n．F(x)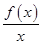＝在(0，＋∞)上是增函数，F(x₁)＜F(x₁＋x₂＋…＋x_n)，即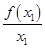＜，而x₁＞0，所以f(x₁)＜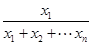f(x₁＋x₂＋…＋x_n)，同理f(x₂)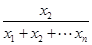＜f(x₁＋x₂＋…＋x_n)，……

f(x_n)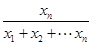＜f(x₁＋x₂＋…＋x_n)，以上n个不等式相加，得f(x₁)＋f(x₂)＋…＋f(x_n)＜f(x₁＋x₂＋…＋x_n)，得证.

试题解析：（Ⅰ）对F(x)求导数，得F′(x)＝．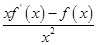

∵f ′(x)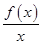＞，x＞0，∴xf ′(x)＞f(x)，即xf ′(x)－f(x)＞0，

∴F′(x)＞0．

故F(x)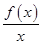＝在(0，＋∞)上是增函数．

（Ⅱ）∵x₁＞0，x₂＞0，∴0＜x₁＜x₁＋x₂．

由（Ⅰ），知F(x)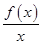＝在(0，＋∞)上是增函数，

∴F(x₁)＜F(x₁＋x₂)，即＜．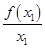

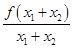∵x₁＞0，∴f(x₁)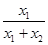＜f(x₁＋x₂)．

同理可得f(x₂)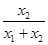＜f(x₁＋x₂)．

以上两式相加，得f(x₁)＋f(x₂)＜f(x₁＋x₂)．

（Ⅲ）（Ⅱ）中结论的推广形式为：

设x₁，x₂，…，x_n∈(0，＋∞)，其中n≥2，则f(x₁)＋f(x₂)＋…＋f(x_n)＜f(x₁＋x₂＋…＋x_n)．

∵x₁＞0，x₂＞0，…，x_n＞0，

∴0＜x₁＜x₁＋x₂＋…＋x_n．

由（Ⅰ），知F(x)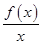＝在(0，＋∞)上是增函数，

∴F(x₁)＜F(x₁＋x₂＋…＋x_n)，即＜．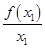

∵x₁＞0，

∴f(x₁)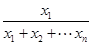＜f(x₁＋x₂＋…＋x_n)．

同理可得

f(x₂)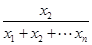＜f(x₁＋x₂＋…＋x_n)，

f(x₃)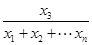＜f(x₁＋x₂＋…＋x_n)，

……

f(x_n)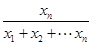＜f(x₁＋x₂＋…＋x_n)．

以上n个不等式相加，得f(x₁)＋f(x₂)＋…＋f(x_n)＜f(x₁＋x₂＋…＋x_n)．

考点：1.利用导数求单调性；2.利用函数单调性证明不等式.