
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
科目:高中数学 来源: 题型:
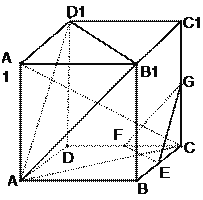
【题目】如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线![]() C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手平时射击成绩统计如表:
环数 | 7环以下 | 7 | 8 | 9 | 10 |
概率 |
| a | b |
|
|
已知他射中7环及7环以下的概率为![]() .
.
![]() 求a和b的值;
求a和b的值;
![]() 求命中10环或9环的概率;
求命中10环或9环的概率;
![]() 求命中环数不足9环的概率.
求命中环数不足9环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点.
恒过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 是非零向量,则“
是非零向量,则“ ![]() ,
, ![]() 共线”是“|
共线”是“| ![]() |+|
|+| ![]() |=|
|=| ![]() +
+ ![]() |”的( )
|”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)满足2x2f(x)+x3f′(x)=ex , f(2)= ![]() ,则x∈[2,+∞)时,f(x)( )
,则x∈[2,+∞)时,f(x)( )
A.有最大值 ![]()
B.有最小值 ![]()
C.有最大值 ![]()
D.有最小值 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)若bn=![]() ,且数列{bn}的前
,且数列{bn}的前![]() 项和为Sn=360,求
项和为Sn=360,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com