Question

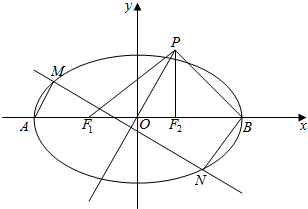
7．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左右焦点分别是F₁，F₂，左、右顶点分别为A、B，焦距为2c，O为坐标原点，点P（c，b）满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$，|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在直线l：y=kx+m与椭圆C交于M、N两点，使得直线PO平分线段MN，且$\overrightarrow{AM}$=λ$\overrightarrow{BN}$？若存在，求l的方程；若不存在，说明理由．

Answer 1

分析 （Ⅰ）求得B（a，0），F₁（-c，0），F₂（c，0），再由向量的坐标，可得a=2c，运用两点的距离公式和a，b，c的关系，解方程可得a，b，进而得到椭圆方程；
（Ⅱ）假设存在直线l：y=kx+m与椭圆C交于M、N两点，使得直线PO平分线段MN，且$\overrightarrow{AM}$=λ$\overrightarrow{BN}$．将椭圆的方程和直线y=kx+m，联立消去y，可得x的方程，运用韦达定理和中点坐标公式，结合向量共线的坐标表示，解方程可得k，m，即可判断存在．

解答 解：（Ⅰ）B（a，0），F₁（-c，0），F₂（c，0），
由$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$，|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$，可得
（-c，-b）+（a-c，-b）=2（0，-b），
即有a=2c，又b²+4c²=7，a²-b²=c²，
解得a=2，b=$\sqrt{3}$，c=1，
则椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1；
（Ⅱ）假设存在直线l：y=kx+m与椭圆C交于M、N两点，
使得直线PO平分线段MN，且$\overrightarrow{AM}$=λ$\overrightarrow{BN}$．
将直线y=kx+m代入椭圆方程，可得（3+4k²）x²+8kmx+4m²-12=0，
判别式△=64k²m²-4（3+4k²）（4m²-12）＞0，
设M（x₁，y₁），N（x₂，y₂），
即有x₁+x₂=-$\frac{8km}{3+4{k}^{2}}$，x₁x₂=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$，
则MN的中点坐标为（-$\frac{4km}{3+4{k}^{2}}$，$\frac{3m}{3+4{k}^{2}}$），
即有3m=-4$\sqrt{3}$km，
若m=0，即直线y=kx经过原点，成立；
若m≠0，则k=-$\frac{\sqrt{3}}{4}$，
由$\overrightarrow{AM}$=λ$\overrightarrow{BN}$，可得（x₁+2）y₂=（x₂-2）y₁，
即为m（x₁-x₂）+2（y₁+y₂）=0，
即有-m$\sqrt{\frac{64{k}^{2}{m}^{2}}{（3+4{k}^{2}）^{2}}-\frac{16{m}^{2}-48}{3+4{k}^{2}}}$+$\frac{12m}{3+4{k}^{2}}$=0，
解方程可得m=±$\frac{\sqrt{3}}{2}$．
检验判别式大于0成立，
故存在，且直线l的方程为y=kx或y=-$\frac{\sqrt{3}}{4}$x±$\frac{\sqrt{3}}{2}$．

点评 本题考查椭圆的方程的求法，注意运用向量的坐标运算，考查直线和椭圆方程联立，运用韦达定理和向量共线的坐标表示，考查运算能力，属于中档题．