
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 、
、![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】“双十二”是继“双十一”之后的又一个网购狂欢节,为了刺激“双十二”的消费,某电子商务公司决定对“双十一”的网购者发放电子优惠券.为此,公司从“双十一”的网购消费者中用随机抽样的方法抽取了100人,将其购物金额(单位:万元)按照![]() ,
, ![]() 分组,得到如下频率分布直方图:
分组,得到如下频率分布直方图:
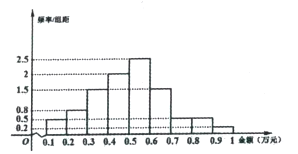
根据调查,该电子商务公司制定了发放电子优惠券的办法如下:

(Ⅰ)求购物者获得电子优惠券金额的平均数;
(Ⅱ)从这100名购物金额不少于0.8万元的人中任取2人,求这两人的购物金额在0.8~0.9万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com