
【题目】若图,在三棱柱 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,且
,且 ![]() 和
和 ![]() 均为正三角形.
均为正三角形.
(1)在 ![]() 上找一点
上找一点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并说明理由.
,并说明理由.
(2)若 ![]() 的面积为
的面积为 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
【答案】
(1)解: ![]() 为
为 ![]() 的中点时,
的中点时, ![]() 平面
平面 ![]() ,
,
如图,
取 ![]() 的中点
的中点 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() ,
,
在三棱柱 ![]() 中,
中, ![]() ,
,
所以四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
,
由已知, ![]() 为正三角形,所以
为正三角形,所以 ![]() ,
,
因为 ![]() 平面
平面 ![]() ,平面
,平面 ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]()
(2)解:设 ![]() 的边长为
的边长为 ![]() ,则
,则 ![]() ,
,
所以 ![]() ,
,
因为三棱柱 ![]() 的体积为三棱锥
的体积为三棱锥 ![]() 体积的
体积的 ![]() 倍,
倍,
所以四棱锥 ![]() 的体积等于三棱锥
的体积等于三棱锥 ![]() 体积的
体积的 ![]() 倍,
倍,
即 ![]() .
.
【解析】(1)根据题意结合已知条件作出辅助线即可得出线线平行进而得到四边形 A1 A O P 为平行四边形故有 A1 P / / A O 再由正三角形的性质得到 A O ⊥ B C再由面面垂直的性质得到线面垂直。(2)结合题意可知四棱锥 A1 B C C1 B1的体积等于三棱锥 A1 A B C 体积的 2 倍代入数值到三棱锥体积的公式求出结果即可。
【考点精析】根据题目的已知条件,利用平面与平面垂直的性质的相关知识可以得到问题的答案,需要掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣ ![]() x2 , 其中a∈R,e为自然对数的底数
x2 , 其中a∈R,e为自然对数的底数
(Ⅰ)函数f(x)的图象能否与x轴相切?若能与x轴相切,求实数a的值;否则,请说明理由;
(Ⅱ)若函数y=f(x)+2x在R上单调递增,求实数a能取到的最大整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R, ![]() +1>3x0”的否定是“x∈R,x2+1≤3x”;
+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量a与b的夹角是钝角”的充要条件是“a·b<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在矩形 ![]() 中,
中, ![]() ,
, ![]() 是
是 ![]() 的中点,将三角形
的中点,将三角形 ![]() 沿
沿 ![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面 ![]()
![]() 平面
平面 ![]() .
.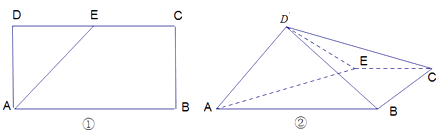
(1)在线段 ![]() 上确定点
上确定点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并证明;
,并证明;
(2)求 ![]() 与
与 ![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两个不同点 ![]() 、
、 ![]() 满足条件:①
满足条件:① ![]() 、
、 ![]() 都在函数
都在函数 ![]() 的图像上;②
的图像上;② ![]() 、
、 ![]() 关于原点对称,则称点对
关于原点对称,则称点对 ![]() 是函数
是函数 ![]() 的一对“友好点对”(注:点对
的一对“友好点对”(注:点对 ![]() 与
与 ![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数 ![]()
 ,则此函数的“友好点对”有( )对.
,则此函数的“友好点对”有( )对.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“抛物线 ![]() 的准线方程为
的准线方程为 ![]() ”是“抛物线
”是“抛物线 ![]() 的焦点与双曲线
的焦点与双曲线 ![]() 的焦点重合”的( )
的焦点重合”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y∈R,且 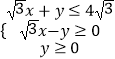 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com