
【题目】已知全集U=R,集合A={x|﹣1≤x≤3},B={x|x2<4},
(1)求A∪B;
(2)求集合UA.
【答案】
(1)解:全集U=R,集合A={x|﹣1≤x≤3},
B={x|x2<4}={x|﹣2<x<2}
A∪B={x|﹣2<x≤3}
(2)解:CUA={x|x<﹣1或x>3}
【解析】(1)化简集合B,根据并集的定义求出A∪B;(2)根据补集的定义求出集合UA.
【考点精析】认真审题,首先需要了解集合的并集运算(并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立),还要掌握集合的补集运算(对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制)的相关知识才是答题的关键.
B,反之也成立),还要掌握集合的补集运算(对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制)的相关知识才是答题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,已知a1=10,a2为整数,且Sn≤S4.
(1)求{an}的通项公式;
(2)设bn=![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= ![]() 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“x∈{x|-1≤x≤1},都有不等式x2-x-m<0成立”是真命题.
(1)求实数m的取值集合B;
(2)设不等式(x-3a)(x-a-2)<0的解集为A,若x∈A是x∈B的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的前n项和为Sn, S3=a4+6,且a1, a4, a13成等比数列.
(1)求数列{an}的通项公式;
(2)设![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
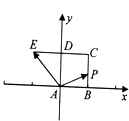
【题目】如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则下列命题正确的是 . (填上所有正确命题的序号)
,则下列命题正确的是 . (填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量 ![]() 和实数x,使
和实数x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com