
【题目】已知集合![]() .
.
(1)若![]() ,求
,求![]() 的概率;
的概率;
(2)若![]() ,求
,求![]() 的概率.
的概率.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)﹣g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2﹣3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx+m,m∈R.
(1)已知函数f(x)在点(l,f(1))处与x轴相切,求实数m的值;
(2)求函数f(x)的单调区间;
(3)在(1)的结论下,对于任意的0<a<b,证明: ![]() <
< ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M﹣BQ﹣C大小为30°,求QM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,![]() .
.

(1)证明: A1BD // 平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人. 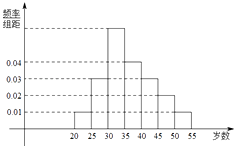
(1)求N和[30,35)这组的参加者人数N1;
(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;
(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com