
分析 (1)根据f(x)=x2-4ax+2a+12(a∈R)的值都是非负的,判别式小于等于0求得a的范围,
(2)根据(1)a的范围确定函数g(a)的解析式,根据函数的单调性求得函数的值域.
解答 解(1)解:依题意可知△=16a2-4(2a+12)≤0,解得-$\frac{3}{2}$≤a≤2;
(2)当1≤a≤2时,g(a)=(a+1)(|a-1|+2)=(a+1)2,单调增,∴g(a)∈[4,9];
当-$\frac{3}{2}$≤a<1时,g(a)=(a+1)(|a-1|+2)=-(a-1)2+4,函数单调增,∴g(a)∈[-$\frac{9}{4}$,4);
综合得函数g(a)的值域为[-$\frac{9}{4}$,9].
点评 本题主要考查了二次函数的值域问题.解题的关键是求得函数的解析式和在定义域上的单调性,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
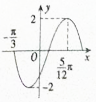 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com