
【题目】如图,在平面直角坐标系中,锐角![]() 和钝角
和钝角![]() 的终边分别与单位圆交于
的终边分别与单位圆交于![]() 两点.
两点.
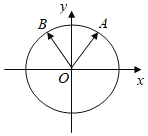
(Ⅰ)如果点![]() 纵坐标分别为
纵坐标分别为![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 为
为![]() 轴上异于
轴上异于![]() 的点,且
的点,且![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用三角函数的定义,结合两角和差的余弦公式进行计算即可;(Ⅱ) 若![]() ,则
,则![]() ,设
,设![]() ,可得
,可得![]() ,利用向量垂直的坐标公式,可得
,利用向量垂直的坐标公式,可得![]() ,由
,由![]() ,结合余弦函数的单调性可得结果.
,结合余弦函数的单调性可得结果.
(Ⅰ)∵点A、B纵坐标分别为![]() 、
、![]() ,
,
∴sinα=![]() ,sinβ=
,sinβ=![]() ,
,
∵α为锐角,β为钝角,
![]()
![]()
(Ⅱ)依题意得A(cosα,sinα),B(cosβ,sinβ),
∵AOB=90,即β=α+90,
∴B(-sinα,cosα),
设![]()
∴(-x+cosα)(-x-sinα)+sinα·cosα=0,
整理得x2+x(sinα-cosα)=0,(x0),
∴x=cosα-sinα=![]() cos(α+
cos(α+![]() ),(x0),
),(x0),
![]()
所以x(-1,0)∪(0,1).


科目:高中数学 来源: 题型:
【题目】双曲线 ![]() 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ![]() ,
, ![]() 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ![]() ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,虚轴长为2.
,虚轴长为2.
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)若直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 两点,(
两点,( ![]() 均异于左、右顶点),且以
均异于左、右顶点),且以![]() 为直径的圆过双曲线
为直径的圆过双曲线![]() 的左顶点
的左顶点![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示 
(1)写出销售价格P(元)和时间t(天)的函数解析式;
(2)若日销售量Q(件)与时间t(天)的函数关系是Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知标有1~20号的小球20个,若我们的目的是估计总体号码的平均值,即20个小球号码的平均值.试验者从中抽取4个小球,以这4个小球号码的平均值估计总体号码的平均值,按下面方法抽样(按小号到大号排序):
(1)以编号2为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
(2)以编号3为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于利用斜二侧法得到的直观图有下列结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是( )
A. ①② B. ① C. ③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 为真,
为真,![]() 为假,
为假,![]() 为真
为真
(2)“![]() ”是“曲线
”是“曲线![]() 表示椭圆”的充要条件
表示椭圆”的充要条件
(3)命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
(4)如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
则正确命题有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com