
 +
+ =1(a>b>0)的右焦点为F(c,0),下顶点为A(0,-b),直线AF与椭圆的右准线交于点B,与椭圆的另一个交点为点C,若F恰好为线段AB的中点.
=1(a>b>0)的右焦点为F(c,0),下顶点为A(0,-b),直线AF与椭圆的右准线交于点B,与椭圆的另一个交点为点C,若F恰好为线段AB的中点. ,求椭圆的方程.
,求椭圆的方程. ,…(2分)
,…(2分) =
= ,所以椭圆的离心率e=
,所以椭圆的离心率e= …(4分)
…(4分) c,b=c,所以直线AB的方程为y=x-c,
c,b=c,所以直线AB的方程为y=x-c,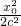 +
+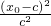 =1,…(6分)
=1,…(6分) +2(x0-c)2=2c2,
+2(x0-c)2=2c2, c.
c. c,
c, c),…(8分)
c),…(8分) ,由两点距离公式可得(
,由两点距离公式可得( c-c)2+(
c-c)2+( c)2=
c)2= ,
, ,
, +
+ =1. …(10分)
=1. …(10分) ,从而可求得椭圆的离心率;
,从而可求得椭圆的离心率; ,可求得c,从而可求得椭圆的方程.
,可求得c,从而可求得椭圆的方程.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
素材2:设f(m)=||AB|-|CD||.
试根据上述素材构建一个问题,然后再解答.
查看答案和解析>>
科目:高中数学 来源: 题型:
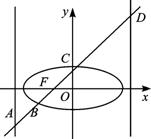
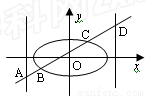
如图,已知椭圆![]() =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||
(1)求f(m)的解析式;
(2)求f(m)的最值.
查看答案和解析>>
科目:高中数学 来源:2014届广东省、阳东一中高二上联考文数试卷(解析版) 题型:解答题
(本题满分14分)
如图,已知椭圆 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.

(1)若∠F1AB=90°,求椭圆的离心率;
(2)若 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三上学期11月月考理科数学卷 题型:解答题
(本小题满分15分)
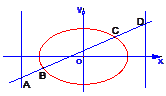
如图,已知椭圆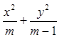 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线
=1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及直线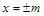 的交点从左到右的顺序为A、B、C、D,设
的交点从左到右的顺序为A、B、C、D,设 .
.
(Ⅰ)求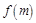 的解析式;
的解析式;
(Ⅱ)求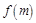 的最值.
的最值.
查看答案和解析>>
科目:高中数学 来源:2010年河南省高二上学期12月份考试数学卷(文理) 题型:解答题
(12分)如图,已知椭圆 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 ,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2, 证明: =2;
=2;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com