
【题目】如图,在△MBC中,MA是BC边上的高,MA=3,AC=4,将△MBC沿MA进行翻折,使得∠BAC=90°如图,再过点B作BD∥AC,连接AD,CD,MD且![]() ,∠CAD=30°.
,∠CAD=30°.
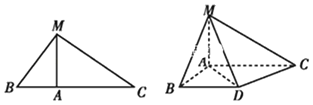
(1)求证:平面MCD⊥平面MAD;
(2)求点B到平面MAD的距离.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)证明CD⊥平面MAD即可.
(2)利用等体积法 VB﹣MAD=VM﹣BAD,再求出![]() ,利用三棱锥的体积公式求解即可.
,利用三棱锥的体积公式求解即可.
(1)因为MA是BC边上的高,所以MA⊥AB,MA⊥AC,
又因为AB平面ABDC,AC平面ABDC,AB∩AC=A,
所以MA⊥平面ABDC,则MA⊥CD,MA⊥AD,
在Rt△ADM中,MD![]() ,
,
在Rt△ACM中,MC![]() 5,
5,
在△ACD中,由余弦定理可得CD![]() 2,
2,
则在△CDM中,CD2+DM2=CM2,即有△CDM是直角三角形,所以CD⊥DM,
又因为CD⊥AM,AM平面MAD,DM平面MAD,AM∩DM=M,
所以CD⊥平面MAD,又因为CD平面MCD,所以平面MCD⊥平面MAD;
(2)在△BAD中,∠BAD=60°,AD=2![]() ,则AB
,则AB![]() ,BD=3,所以
,BD=3,所以![]() ,
,
又因为MA⊥AD,所以![]() 3
3![]() ,
,
因为MA⊥平面ABDC,即MA⊥平面BAD,则VB﹣MAD=VM﹣BAD,
即![]() 3
3![]() ,解得d
,解得d![]() ,
,
即点B到平面MAD的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
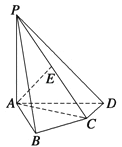
(1)求PB和平面PAD所成的角的大小;
(2)证明AE⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
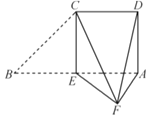
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AB的中点
,E为AB的中点![]() 将
将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
![]() 求证:平面
求证:平面![]() 平面AEF;
平面AEF;
![]() 求直线DF与平面CEF所成角的正弦值.
求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com