
【题目】执行如图所示的程序框图,则输出的k的值是( )
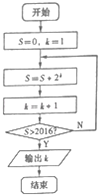
A.10 B.11 C.12 D.13
【答案】A
【解析】解:第1次执行循环体后,S=2,k=2,不满足退出循环的条件,
第2次执行循环体后,S=6,k=3,不满足退出循环的条件,
第3次执行循环体后,S=14,k=4,不满足退出循环的条件,
第4次执行循环体后,S=30,k=5,不满足退出循环的条件,
第5次执行循环体后,S=62,k=6,不满足退出循环的条件,
第6次执行循环体后,S=126,k=7,不满足退出循环的条件,
第7次执行循环体后,S=510,k=8,不满足退出循环的条件,
第8次执行循环体后,S=1022,k=9,不满足退出循环的条件,
第9次执行循环体后,S=2046,k=10,满足退出循环的条件,
故输出的k值为10,
故选:A


科目:高中数学 来源: 题型:
【题目】如图,某同学在素质教育基地通过自己设计、选料、制作,打磨出了一个作品,作品由三根木棒![]() ,
,![]() ,
,![]() 组成,三根木棒有相同的端点
组成,三根木棒有相同的端点![]() (粗细忽略不计),且
(粗细忽略不计),且![]() 四点在同一平面内,
四点在同一平面内,![]()
![]() ,
,![]() ,木棒
,木棒![]() 可绕点O任意旋转,设BC的中点为D.
可绕点O任意旋转,设BC的中点为D.
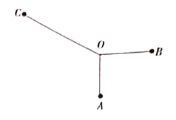
(1)当![]() 时,求OD的长;
时,求OD的长;
(2)当木棒OC绕点O任意旋转时,求AD的长的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且
,且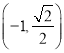 在椭圆E上.
在椭圆E上.
(1)求椭圆E的标准方程;
(2)已知垂直于x轴的直线![]() 交E于A、B两点,垂直于y轴的直线
交E于A、B两点,垂直于y轴的直线![]() 交E于C、D两点,
交E于C、D两点,![]() 与
与![]() 的交点为P,且
的交点为P,且![]() ,间:是否存在两定点M,N,使得
,间:是否存在两定点M,N,使得![]() 为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
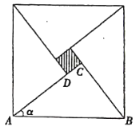
【题目】三国时期吴国的数学家赵爽曾创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个全等的直角三角形与中间的小正方形拼成一个大正方形,其中一个直角三角形中较小的锐角![]() 满足
满足![]() ,现向大正方形内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
,现向大正方形内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com