
【题目】已知函数![]() .
.
(1)若![]() ,求函数f(x)的单调递增区间;
,求函数f(x)的单调递增区间;
(2)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】在湖北新冠疫情严重期间,我市响应国家号召,召集医务志愿者组成医疗队驰援湖北.某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加,医院计划从医生和护士中各选2名参加医疗队.
(1)求选出的4名志愿全是女性的选派方法数;
(2)记![]() 为选出的4名选手中男性的人数,求
为选出的4名选手中男性的人数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利![]() 元,求
元,求![]() 的分布列,并求出均值
的分布列,并求出均值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
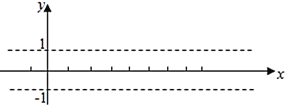
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】你知道吗,生产甲流H1N1流感疫苗的最主要原材料居然是鸡蛋!不过这可不是一种普通的鸡蛋,而是一种原产于美国的海兰白鸡蛋.工人们首先在强光照射下,挑选出“受过精”的鸡蛋,未“受过精”的鸡蛋只能作为普通食用蛋走上市场,这个过程叫做“照检”照检挑选出来的鸡蛋被送到疫苗生产车间,先经过严格的消毒,然后这些鸡蛋里面被植入由世卫组织提供的甲流毒株,这些接受了毒株的鸡蛋将被放置在特殊环境的车间里,使得毒株在鸡蛋里迅速生长,大约3天后,就“成熟”了.这时鸡蛋转到另一车间进行毒株的“收获”.鸡蛋里的羊水是我们需要的所谓的“病毒收获液”,剩下的蛋壳和未发育完整的小鸡将被高温消毒后送到其他企业,制成饲料.病毒收获液里含有我们需要的抗病毒成分,再依次经过了灭活、纯化、裂解后,就得到了我们需要的甲流疫苗了.下面是以上整个生产过程的流程图,则图中的①②位置上应分别填上( )
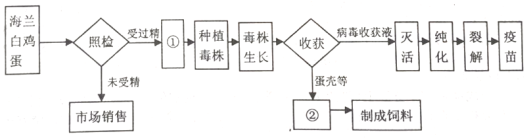
A.消毒、消毒B.挑选、消毒C.消毒、裂解D.消毒、挑选
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com