【题目】如图，直角梯形ABDC中，
，
，
，
，
.
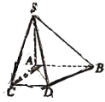
（1）若S是直角梯形ABDC所在平面外一点，画出平面SBD和平面SAC的交线，并说明理由；
（2）直角梯形ABDC绕直线AC所在直线旋转一周所得几何体名称是什么?并求出其体积.
【答案】(1)交线和理由见详解；(2)所得几何体为圆台，体积为
.
【解析】
（1）找到两个平面的两个公共点，根据公理，即可得到交线；
（2）根据旋转体的特点，即可知道几何体的名称，根据圆台体积计算公式可算出体积.
（1）根据题意，平面SBD和平面SAC的交线为
，具体如下图所示：
延长AC，延长BD，取两条直线的交点为M，连接SM，
则SM即为平面SBD和平面SAC的交线为
理由如下：
因为S点在平面SAC中，S点也在平面SBD中，
故S点为两平面的公共点；
又因为M点在直线AC上，直线AC在平面SAC中，
故M点在平面SAC中；
同理，因为M点在直线BD上，直线BD在平面SBD中，
故M点在平面SBD中；
则M点和S点均是平面SAC和平面SBD的公共点
故直线SM为两个平面的交线.
（2）该旋转体为圆台.
其中小圆的圆面积为
大圆的圆面积为
圆台的高即为AC的长度，故
则该圆台的体积为
解得
故该几何体为圆台，且体积为.
100分闯关期末冲刺系列答案科目：高中数学 来源： 题型：
【题目】某地区某农产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根据表中数据，建立
关于的线性回归方程
；
（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据
，其回归直线的斜率和截距的最小二乘估计分别为：
，
.(参考数据:
，计算结果保留小数点后两位）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】进入12月以来，某地区为了防止出现重污染天气，坚持保民生、保蓝天，严格落实机动车限行等一系列“管控令”，该地区交通管理部门为了了解市民对“单双号限行”的赞同情况，随机采访了220名市民，将他们的意见和是否拥有私家车情况进行了统计，得到如下的2×2列联表：
| 赞同限行 | 不赞同限行 | 合计 |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
（1）根据上面的列联表判断，能否有99%的把握认为“赞同限行与是否拥有私家车”有关；
（2）为了解限行之后是否对交通拥堵、环境污染起到改善作用，从上述调查的不赞同限行的人员中按分层抽样抽取6人，再从这6人中随机抽出2名进行电话回访，求抽到的2人中至少有1名“没有私家车”人员的概率．
参考公式：K2＝
P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3..841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝
，g(x)＝
(a>0，且a≠1).
(1)求函数φ(x)＝f(x)＋g(x)的定义域；
(2)试确定不等式f(x)≤g(x)中x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
