
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 在线段
在线段![]() 上运动,设
上运动,设![]() .
.
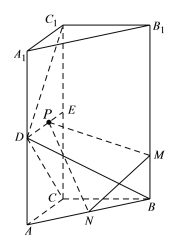
(1)证明:![]() ;
;
(2)是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】为增强学生法治观念,营造“学宪法、知宪法、守宪法”的良好校园氛围,某学校开展了“宪法小卫士”活动,并组织全校学生进行法律知识竞赛.现从全校学生中随机抽取50人,统计他们的竞赛成绩,并得到如表所示的频数分布表.
分数段 |
|
|
|
|
|
人数 | 5 | 15 | 15 | 12 |
|
(Ⅰ)求频数分布表中的![]() 的值,并估计这50名学生竞赛成绩的中位数(精确到0.1);
的值,并估计这50名学生竞赛成绩的中位数(精确到0.1);
(Ⅱ)将成绩在![]() 内定义为“合格”,成绩在
内定义为“合格”,成绩在![]() 内定义为“不合格”.请将列联表补充完整.
内定义为“不合格”.请将列联表补充完整.
合格 | 不合格 | 合计 | |
高一新生 | 12 | ||
非高一新生 | 6 | ||
合计 |
试问:是否有95%的把握认为“法律知识的掌握合格情况”与“是否是高一新生”有关?说明你的理由;
(Ⅲ)在(Ⅱ)的前提下,在该50人中,按“合格与否”进行分层抽样,随机抽取5人,再从这5人中随机抽取2人,求恰好2人都合格的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
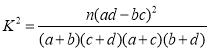 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程是
中,直线l的参数方程是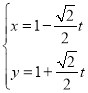 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是![]() .
.
(1)证明:直线l与曲线C相切;
(2)设直线l与x轴、y轴分别交于点A,B,点P是曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买![]() 台机器人的总成本
台机器人的总成本![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排![]() 人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量
人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量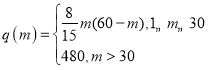 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少多少?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考,取消文理科,实行“![]() ”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在
”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年),并把调查结果制成下表:
称为中老年),并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)分别估计中青年和中老年对新高考了解的概率;
(2)请根据上表完成下面![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 截直线
截直线![]() 所得的线段的长度为
所得的线段的长度为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com