
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
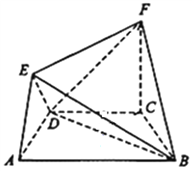
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析;(2)直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
【解析】试题分析:(1)要证线面平行,先找线线平行,先证平面AED⊥平面ABCD,做过E作EG⊥AD于G,则EG⊥平面ABCD,∴FC∥EG,进而得到线面平行;(2)建系,求面的法向量和线的方向向量,根据向量夹角得到线面角,即可。
解析:
(Ⅰ)证明:∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴BC=DC,∠ADC=∠BCD=120°,∴∠CDB=30°,
∴∠ADB=90°,即BD⊥AD.
又AE⊥BD, ![]() =A,∴BD⊥平面AED,
=A,∴BD⊥平面AED,
又BD![]() 平面ABCD,∴平面AED⊥平面ABCD.
平面ABCD,∴平面AED⊥平面ABCD.
如图4,过E作EG⊥AD于G,则EG⊥平面ABCD,
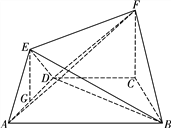
又FC⊥平面ABCD,∴FC∥EG.
又EG![]() 平面AED,FC
平面AED,FC![]() 平面AED,
平面AED,
∴FC∥平面AED.
(Ⅱ)解:如图5,连接AC,由(Ⅰ)知AC⊥BC,
∵FC⊥平面ABCD,
∴CA,CB,CF两两垂直.
以C为原点,建立空间直角坐标系Cxyz.
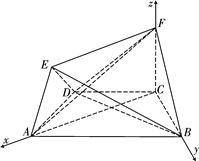
设BC![]() ,则AC
,则AC![]() ,AB
,AB![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,
, ![]() .
.
设平面BDF的法向量为![]() ,
,
则![]() 即
即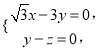
令![]() ,则
,则![]() ,
, ![]() ,则
,则![]() .
.
设直线AF与平面BDF所成角为![]() ,则
,则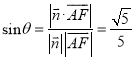 ,
,
故直线AF与平面BDF所成角的余弦值为![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
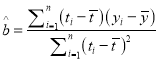 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 为矩形,四边形
为矩形,四边形![]() 为梯形,
为梯形, ![]() ,平面
,平面![]() 与平面
与平面![]() 垂直,且
垂直,且![]() .
.
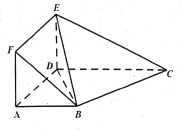
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,且平面
,且平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]() 满足:
满足: ![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
, ![]() 为前
为前![]() 项
项![]() ,
, ![]() ,
, ![]() ,
, ![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(Ⅰ)若![]() ,请写出数列
,请写出数列![]() 的前7项;
的前7项;
(Ⅱ)求证:对于任意正整数![]() ,必存在
,必存在![]() ,使得
,使得![]() ;
;
(Ⅲ)求证:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]()
![]() 成立”的充要条件。
成立”的充要条件。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·太原三模)已知等比数列{an}的各项均为不等于1的正数,数列{bn}满足bn=lgan,b3=18,b6=12,则数列{bn}的前n项和的最大值为( )
A. 126 B. 130 C. 132 D. 134
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N的距离的![]() 倍.
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线![]() :x﹣my﹣1=0交曲线E于A,C两点,直线
:x﹣my﹣1=0交曲线E于A,C两点,直线![]() :mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
:mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
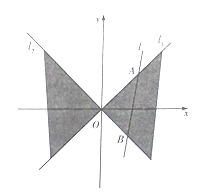
【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分即为
之间的阴影部分即为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与轨迹
与轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证: ![]() 的面积恒为定值.
的面积恒为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com