
(本大题满分14分)
设函数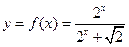 上两点
上两点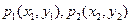 ,若
,若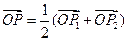 ,且P点的横坐标为
,且P点的横坐标为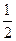 .
.
(1)求P点的纵坐 标;
标;
(2)若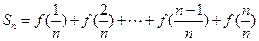 求
求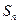 ;
;
(3)记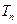 为数列
为数列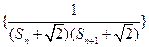 的前n项和,若
的前n项和,若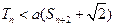 对一切
对一切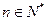 都成立,试求a的取值范围.
都成立,试求a的取值范围.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某种型号的汽车在匀速行驶中每小时耗油量y (升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: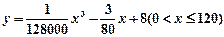 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀 速行驶时,从甲地到乙地要耗油多少升?
速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 ,
,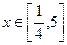 , 其中
, 其中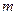 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出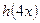 的定义域(2分);
的定义域(2分);
(文)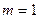 时,直接写出
时,直接写出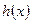 的值域(4分)
的值域(4分)
(2)、(文、理)求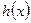 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数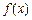
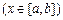 ,定义:
,定义: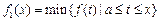
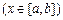 ,
,
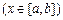 .其中,
.其中, 表示函数
表示函数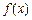 在
在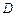 上的最小值,
上的最小值,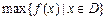 表示函数
表示函数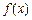 在
在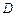
 上的最大值.例如:
上的最大值.例如: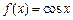 ,
,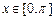 ,则
,则 ,
,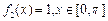 ,
,
(理)当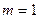 时,设
时,设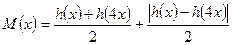 ,不等式
,不等式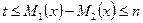
恒成立,求 的取值范围(11分);
的取值范围(11分);
(文)当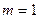 时,
时,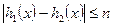 恒成立,求
恒成立,求 的取值范围(8分);
的取值范围(8分);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知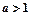 ,函数
,函数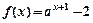
(1)求 的反函数
的反函数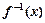 ;
;
(2)若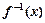 在[0,1]上的最大值与最小值互为相反数,求
在[0,1]上的最大值与最小值互为相反数,求 ;
;
(3)若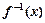 的图像不经过第二象限,求
的图像不经过第二象限,求 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知函数f(x)=-x2+ax-lnx(a∈R).
(1)求函数f(x)既有极大值又有极小值的充要条件;
(2)当函数f(x)在[,2]上单调时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数
 ,其图象过点(
,其图象过点( ,
, ).
).
(1)求 的值及
的值及 最小正周期;
最小正周期;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数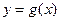 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com