
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且当
,且当![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
(1)求![]() 的解析式及单调增区间;
的解析式及单调增区间;
(2)若![]() ,且
,且![]() ,求
,求![]() ;
;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 是偶函数,求
是偶函数,求![]() 的最小值.
的最小值.
【答案】(1)![]() (
(![]() );(2)
);(2)![]() ,
, ![]() ,
, ![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)利用函数的周期、最值,求出![]() ,然后求出
,然后求出![]() ,通过当
,通过当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,求出
,求出![]() ,从而求
,从而求![]() 的解析式,解不等式
的解析式,解不等式![]() 可得单调增区间;(2)若
可得单调增区间;(2)若![]() ,且
,且![]() ,可得
,可得![]() 或
或![]() ,
, ![]() 取特殊值可求出
取特殊值可求出![]() ;(3)利用函数
;(3)利用函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,由
的图象,由![]() 是偶函数,可得
是偶函数,可得![]() (
(![]() ),解得
),解得![]() ,然后再求
,然后再求![]() 的最小值.
的最小值.
试题解析:(1)由已知条件知, ![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由![]() (
(![]() ) ,得
) ,得![]() (
(![]() )
)
所以![]() 的单调增区间是
的单调增区间是![]() (
(![]() )
)
(2)由![]() ,得
,得![]() ,
,
所以![]() 或
或![]() (
(![]() )
)
所以![]() 或
或![]() (
(![]() )
)
又![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 或
或![]() .
.
(3)有条件,可得![]()
又![]() 是偶函数,所以
是偶函数,所以![]() 的图象关于
的图象关于![]() 轴对称,所以当
轴对称,所以当![]() 时,
时, ![]() 取最大值或最小值.
取最大值或最小值.
即![]() ,所以
,所以![]() (
(![]() ),解得
),解得![]() (
(![]() )
)
又![]() ,所以
,所以![]() 的最小值是
的最小值是![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点.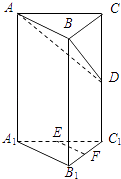
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ ![]() 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足bcosC+ ![]() c=a.
c=a.
(1)求△ABC的内角B的大小;
(2)若△ABC的面积S= ![]() b2 , 试判断△ABC的形状.
b2 , 试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com