
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若函数![]() 的极小值为
的极小值为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明:当
,证明:当![]() 时,
时,![]() 成立.
成立.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求出函数的导数,分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时可得到
时可得到![]() ,令
,令![]() ,根据函数的单调性求出a的值即可;
,根据函数的单调性求出a的值即可;
(2)要证原不等式即证![]() ,然后利用导数分别证明不等式
,然后利用导数分别证明不等式![]() 和
和![]() 即可.
即可.
(1)函数![]() 的定义域是R,
的定义域是R,![]()
![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,
∴![]() 在R上单调递减,函数无极值,
在R上单调递减,函数无极值,
![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 时,
时,![]() 取极小值-1,
取极小值-1,
∴![]() ,即
,即![]() ,
,
令![]() ,
,
则![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴
,∴![]() ;
;
(2)∵![]() ,∴
,∴![]()
∴![]() ,
,
令![]()
∴![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 时,
时,![]() 取得极小值,
取得极小值,
又∵![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∵![]() ,∴
,∴![]() ,
,
∴![]() 时,
时,![]() ,即
,即![]() ,
,
令![]() ,
,
则![]() 对于
对于![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即当
,即当![]() 时,
时,![]() ,
,
∴![]() 时,
时,![]() ,
,
∴![]()
故![]() 时,
时,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,单位:分钟)将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图如图所示:
分组,制成频率分布直方图如图所示:
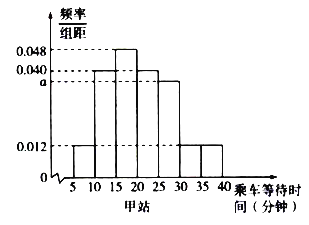
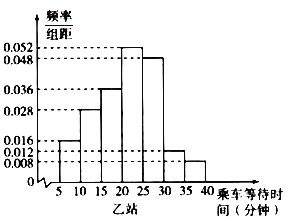
(1)求a的值;
(2)记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着现代电子技术的迅猛发展,关于元件和系统可靠性的研究已发展成为一门新的学科——可靠性理论.在可靠性理论中,一个元件正常工作的概率称为该元件的可靠性.元件组成系统,系统正常工作的概率称为该系统的可靠性.现有![]() (
(![]() ,
,![]() )种电子元件,每种2个,每个元件的可靠性均为
)种电子元件,每种2个,每个元件的可靠性均为![]() (
(![]() ).当某元件不能正常工作时,该元件在电路中将形成断路.现要用这
).当某元件不能正常工作时,该元件在电路中将形成断路.现要用这![]() 个元件组成一个电路系统,有如下两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作.
个元件组成一个电路系统,有如下两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作.
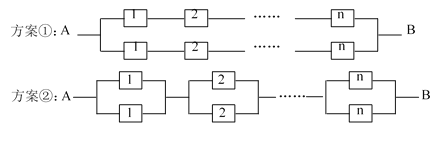
(1)(i)分别写出按方案①和方案②建立的电路系统的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比较![]() 与
与![]() 的大小,说明哪种连接方案更稳定可靠;
的大小,说明哪种连接方案更稳定可靠;
(2)设![]() ,
,![]() ,已知按方案②建立的电路系统可以正常工作,记此时系统中损坏的元件个数为
,已知按方案②建立的电路系统可以正常工作,记此时系统中损坏的元件个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com