
 ,
, ,
, ,
, ,(10分)
,(10分) 与
与 的夹角为θ,则
的夹角为θ,则 .设
.设 与
与 的夹角为θ,则
的夹角为θ,则 .
. . (14分)
. (14分)

 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
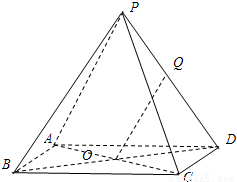
 (2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(2007•静安区一模)(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.查看答案和解析>>
科目:高中数学 来源: 题型:
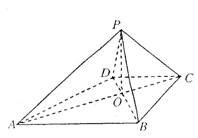
(08年滨州市质检三理) 如图,已知四棱锥P―ABCD的底面ABCD为等腰三角梯形,AB∥CD,AC⊥BC,AC∩BD=0,且顶点P在底面上的射影恰为O点,又OB=2,OP=![]() ,PD⊥PD.
,PD⊥PD.
(1)求二面角B―PA―D的余弦的绝对值;
(2)在棱PC上是否存在点M,使PC⊥平面BMD?若存在,求出点M的位置;若不存在,试说明理由。
(3)在(2)的条件下,求三棱锥C―BMD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年湖北鄂州5月模拟理)(12分)如图,已知四棱锥P―ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60o,E、F 分别是BC、PC的中点.
⑴证明:AE⊥PD;
⑵若H为PD上的动点,EH与平面PAD所成最大角的正
切值为![]() ,求二面角E―AF―C的余弦值.
,求二面角E―AF―C的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
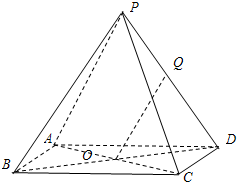 (理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.
(理) 如图,已知四棱锥P-ABCD的底面ABCD是边长为a的正方形,点O为该正方形的中心,侧棱PA=PC,PB=PD.查看答案和解析>>
科目:高中数学 来源: 题型:
(山东卷理)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,![]() ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
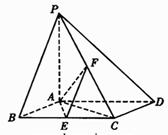 (Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为![]() ,求二面角E—AF—C的余弦值.
,求二面角E—AF—C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com