
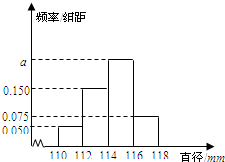
 ij���������IJ�ƷA��ֱ����λ������[110��118]�ڣ���λ��mm����������һ����ƷA��ֱ��λ������[110��112����[112��114����[114��116����[116��118]�ڸó��ɻ����ֱ�Ϊ10��30��20��10����λ��Ԫ�����ִӸó������IJ�ƷA�������ȡ200���������ǵ�ֱ�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ij���������IJ�ƷA��ֱ����λ������[110��118]�ڣ���λ��mm����������һ����ƷA��ֱ��λ������[110��112����[112��114����[114��116����[116��118]�ڸó��ɻ����ֱ�Ϊ10��30��20��10����λ��Ԫ�����ִӸó������IJ�ƷA�������ȡ200���������ǵ�ֱ�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ�����a�ó�����һ��A��Ʒ��ƽ������
��2����Ƶ�ʷֲ�ֱ��ͼ��Ӧ��ֱ��λ������[112��114���IJ�Ʒ���г�ȡ2������ֱ��λ������[114��116���IJ�Ʒ�г�ȡ3�����ɴ������оٷ������������Ʒ��������һ����Ʒ��ֱ��λ������[114��116���ڵĸ��ʣ�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���ã�
2��0.050+0.150+a+0.075��=1��
���a=0.225��
ֱ��λ������[110��112����Ƶ��Ϊ200��2��0.050=20��
λ������[112��114����Ƶ��Ϊ200��2��0.150=60��
λ������[114��116����Ƶ��Ϊ200��2��0.225=90��
λ������[116��118����Ƶ��Ϊ200��2��0.075=30��
��ó�����һ��A��Ʒ��ƽ������Ϊ��
$\frac{10��20+30��60+20��90+10��30}{200}$=20.5��Ԫ����
��2����Ƶ�ʷֲ�ֱ��ͼ�ã�
ֱ��λ������[112��114����[114��116����Ƶ��֮��Ϊ��2��3��
��Ӧ��ֱ��λ������[112��114���IJ�Ʒ���г�ȡ2������ΪA��B��
��ֱ��λ������[114��116���IJ�Ʒ�г�ȡ3������Ϊa��b��c��
������ȡ���������п��ܵ�ȡ���У�
��A��B������A��a������A��b������A��c������B��a������B��b������B��c������a��b������a��c��������b��c������10�֣�
����������Ʒ��������һ����Ʒ��ֱ��λ������[114��116���ڵ�ȡ����7�֣�
��������Ʒ��������һ����Ʒ��ֱ��λ������[114��116���ڵĸ���p=$\frac{m}{n}=\frac{7}{10}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪע���оٷ��ĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��310-1��2 | B�� | $\frac{{{9^{10}}-1}}{2}$ | C�� | 910-1 | D�� | $\frac{{{3^{10}}-1}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-$\frac{��}{6}$ | B�� | x=$\frac{��}{3}$ | C�� | x=-$\frac{��}{12}$ | D�� | x=$\frac{��}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | -$\frac{2\sqrt{2}}{2}$ | D�� | $\frac{2\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��y | B�� | x��y | C�� | x��y | D�� | x��y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com