(本小题满分12分)
数列
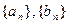
满足:
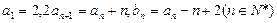
(1)求数列
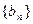
的通项公式;(2)设数列
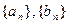
的前n项和分别为A
n、B
n,问是否存在实数
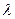
,使得
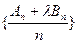
为等差数列?若存在,求出
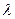
的值;若不存在,说明理由。
解:(1)由

……………………1分
∵
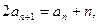
∴
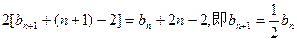
………………4分
∴
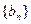
是首项为
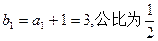
是等比数列。
故
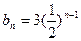
……………………6分
(2)∵
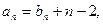
∴
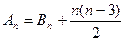
……………………8分
又
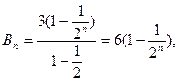
∴
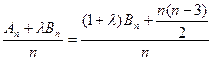
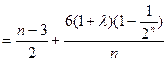
………………10分
故当且仅当
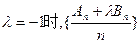
为等差数列……………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分8分)
已知数列

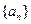
(
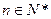
)的前
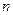
项的
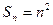
.
(Ⅰ)求数列
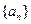
的通项公式;
(Ⅱ)若
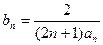
,记数列
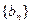
的前n项和为
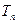
,求使
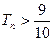
成立的最小正整数n的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题14分)在数列
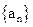
中,
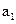
=0,且对任意k
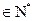
,
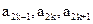
成等差数列,其公差为2k. (Ⅰ)证明
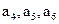
成等比数列;
(Ⅱ)求数列
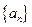
的通项公式;
(Ⅲ)记
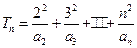
. 证明: 当
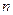
为偶数时, 有
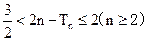
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知奇函数
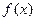
的定义域为
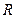
,且是以2为周期的周期函数,数列
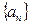
是首项为1,公差为1的等差数列,则
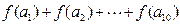
的值为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
数列
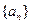
满足
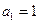
,
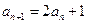
,则数列
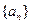
的通项公式为…………………………………( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设等差数列
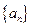
的前n项和为
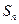
,若
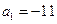
,
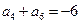
,则当
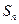
取最小值时,n等于
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
(文)已知数列{
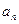
}满足
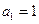
,且
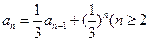
,且
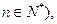
则数列{
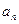
}的通项公式为
查看答案和解析>>

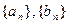 满足:
满足: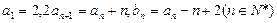
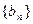 的通项公式;(2)设数列
的通项公式;(2)设数列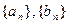 的前n项和分别为An、Bn,问是否存在实数
的前n项和分别为An、Bn,问是否存在实数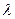 ,使得
,使得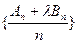 为等差数列?若存在,求出
为等差数列?若存在,求出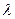 的值;若不存在,说明理由。
的值;若不存在,说明理由。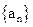 中,
中,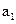 =0,且对任意k
=0,且对任意k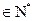 ,
,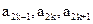 成等差数列,其公差为2k. (Ⅰ)证明
成等差数列,其公差为2k. (Ⅰ)证明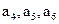 成等比数列;
成等比数列;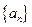 的通项公式;
的通项公式; 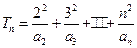 . 证明: 当
. 证明: 当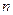 为偶数时, 有
为偶数时, 有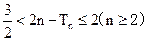 .
.