求经过点A(-2,-1),B(6,-5),且圆心在直线x+y-2=0上的圆的方程.
解:线段AB中点M的坐标为(2,-3),K
AB=
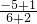
=-

,
故线段AB的中垂线的方程为 y+3=2(x-2),即 y=2x-7,
于是,解方程组
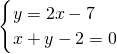
求得圆心坐标为(3,-1),
故圆的半径 r
2=(6-3)
2+(-5+1)
2=25,所以所求圆的方程为 (x-3)
2+(y+1)
2=25.
分析:求出线段AB的中点M的坐标和线段AB的斜率,即得AB的中垂线的斜率,用点斜式求AB的中垂线的方程,将此方程与
直线x+y-2=0 联立方程组,求得圆心的坐标,利用两点间的距离公式求得半径,即可求出圆的标准方程.
点评:本题考查用点斜式求直线的方程,求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键.

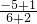 =-
=- ,
,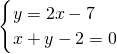 求得圆心坐标为(3,-1),
求得圆心坐标为(3,-1),

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案