
【题目】某人某天的工作是:驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() 三地之间各路段行驶时间及当天降水概率如下表:
三地之间各路段行驶时间及当天降水概率如下表:
路段 | 正常行驶所需时间(小时) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,则在该路段行驶的时间需延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事,然后到达
地办事,然后到达![]() 地, 下午在
地, 下午在![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办事后返回
地,办事后返回![]() 地.设此人8点从
地.设此人8点从![]() 地出发,在各地办事及午餐的累积时间为2小时.
地出发,在各地办事及午餐的累积时间为2小时.
现采用随机数表法获取随机数并进行随机模拟试验,按照以下随机数表,以方框内的数字5为起点,从左向右依次读取数据,若到达某行最后一个数字,则从下一行最左侧数字继续读取,每次读取4位随机数,第1位数表示采取的方案,其中0-4表示采用方案甲,5-9表示采用方案乙;第2-4位依次分别表示当天行驶的三个路段上是否降水,若某路段降水概率为![]() ,则
,则![]() 表示降水,
表示降水,![]() 表示不降水.(符号
表示不降水.(符号![]() 表示的数集包含
表示的数集包含![]() )
)
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23099842 99 64 61 71 6299 15 06![]() 1 29 169358 05 77 05 91
1 29 169358 05 77 05 91
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(1)利用数据“5129”模拟当天的情况,试推算他当日办完事返回![]() 地的时间;
地的时间;
(2)利用随机数表依次取出采用甲、乙方案的模拟结果各两组,分别计算甲、乙两个方案的平均时间,并回答哪个方案办完事后能尽早返回![]() 地.
地.
【答案】(1)19点;(2)甲方案有利于办完事后能更早返回![]() 地.
地.
【解析】
(1)数据“5129”表示采用乙方案,上午![]() 路段降水,下午
路段降水,下午![]() 路段降水,
路段降水,![]() 路段未降水,由此能求出结果.
路段未降水,由此能求出结果.
(2)根据规划,读取的两组甲方案对应数据依次为1693,2687,求出平均时间为10,读取的两组乙方案对应数据为5129,5805,求出平均时间为11,从而认为甲方案有利于办完事后能更早返回![]() 地.
地.
解:(1)数据“5129”表示采用乙方案,上午![]() 路段降水,下午
路段降水,下午![]() 路段降水,
路段降水,![]() 路段未降水,故花费正常行驶时间7小时,降水延迟2小时,办事及午餐2小时共计11小时,
路段未降水,故花费正常行驶时间7小时,降水延迟2小时,办事及午餐2小时共计11小时,
故推算返回![]() 地的时间为19点;
地的时间为19点;
(2)根据规则,读取的两组甲方案对应数据依次为1693,2687,得
数据 | 上午 | 上午 | 下午 | 总时间 | 平均时间 |
1693 | 否 | 否 | 是 | 10 | 10 |
2687 | 否 | 否 | 是 | 10 |
类似地,读取的两组乙方案对应数据为5129,5805,可得
数据 | 上午 | 上午 | 下午 | 总时间 | 平均时间 |
5129 | 是 | 是 | 否 | 11 | 11 |
5805 | 否 | 是 | 是 | 11 |
因为10<11,故认为甲方案有利于办完事后能更早返回![]() 地.
地.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点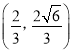
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 是椭圆短轴的一个顶点,并且
是椭圆短轴的一个顶点,并且![]() 是面积为
是面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,已知点
,已知点![]() ,问直线
,问直线![]() 与
与![]() 的交点的横坐标是否为定值?若是,则求出该定值;若不是,请说明理由.
的交点的横坐标是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
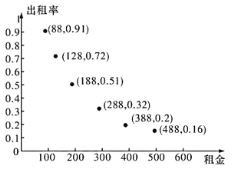
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把活跃网店数量较多的村庄称为淘宝村,随着电子商务在中国的发展,不少农村出现了一批专业的淘宝村,已知某乡镇有多个淘宝村,现从该乡镇淘宝村中随机抽取![]() 家商户,统计他们某一周的销售收入,结果统计如下:
家商户,统计他们某一周的销售收入,结果统计如下:
销售收入(收入) |
|
|
|
|
商户数 |
|
|
|
|
(1)从这![]() 家商户中按该周销售收入超过
家商户中按该周销售收入超过![]() 万元与不超过
万元与不超过![]() 万元分为
万元分为![]() 组,按分层抽样从中抽取
组,按分层抽样从中抽取![]() 家参加经验交流会,并从这
家参加经验交流会,并从这![]() 家中选
家中选![]() 家进行发言,求选出的
家进行发言,求选出的![]() 家恰有
家恰有![]() 家销售收入超过
家销售收入超过![]() 万元的概率;
万元的概率;
(2)若这![]() 家商户中有
家商户中有![]() 家商户入驻两家网购平台,其中
家商户入驻两家网购平台,其中![]() 家销售收入高于
家销售收入高于![]() 万元,完成下面的
万元,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“销售收入是否高于
的把握认为“销售收入是否高于![]() 万元与入驻两家网购平台有关”?
万元与入驻两家网购平台有关”?
入驻两家网购平台 | 仅入驻一家网购平台 | 合计 | |
销售收入高于 | |||
销售收入不高于 | |||
合计 |
附: .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,对角线AC与BD交于点O,
中,底面四边形ABCD是菱形,对角线AC与BD交于点O,![]() .
.
![]() 求证:平面
求证:平面![]() 平面PBD;
平面PBD;
![]() 若
若![]() ,
,![]() ,
,![]() ,E为线段PA的中点,求二面角
,E为线段PA的中点,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com