
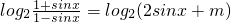 ,x∈(0,π)有实数解,则实数m的取值范围________.
,x∈(0,π)有实数解,则实数m的取值范围________.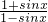 =2sinx+m,
=2sinx+m,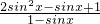
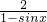 -3≥1,
-3≥1,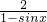 ,即sinx=0时,取等号,
,即sinx=0时,取等号, ,(当且仅当a=b时取等号,且其中a与b必须为正数),本题注意由x的范围,得到sinx≠0,进而得到m≠1.
,(当且仅当a=b时取等号,且其中a与b必须为正数),本题注意由x的范围,得到sinx≠0,进而得到m≠1. 

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com