
【题目】设连续掷两次骰子得到的点数分别为m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(2)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(3)使得事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”发生的概率.
与圆(x﹣3)2+y2=1相交”发生的概率.
【答案】
(1)解:由题意知,m∈{1,2,3,4,5,6};n∈{1,2,3,4,5,6},
故(m,n)所有可能的取法共6×6=36种
使得 ![]() ,即m﹣3n=0,
,即m﹣3n=0,
即m=3n,共有2种(3,1)、(6,2),
所以求使得 ![]() 的概率
的概率 ![]()
(2)解: ![]() 即m2+n2≤10,
即m2+n2≤10,
共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种
使得 ![]() 的概率
的概率 ![]()
(3)解:由直线与圆的位置关系得, ![]() ,
,
即 ![]() ,
,
共有 ![]() ,5种,
,5种,
所以直线 ![]() 与圆(x﹣3)2+y2=1相交的概率
与圆(x﹣3)2+y2=1相交的概率 ![]()
【解析】(1)利用乘法计数原理求出所有可能的取法,利用向量垂直的充要条件得到m﹣3n=0,通过列举法得到得事件“ ![]() ”发生基本事件个数,利用古典概型的概率求出求出值.(2)利用向量模的公式将事件
”发生基本事件个数,利用古典概型的概率求出求出值.(2)利用向量模的公式将事件 ![]() ”转化为m2+n2≤10,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.(3)由直线与圆的位置关系将事件“直线
”转化为m2+n2≤10,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.(3)由直线与圆的位置关系将事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”转化为
与圆(x﹣3)2+y2=1相交”转化为 ![]() ,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.
,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.
【考点精析】本题主要考查了数量积判断两个平面向量的垂直关系的相关知识点,需要掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直才能正确解答此题.
两平面的法向量垂直才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx,g(x)=|x﹣1|,若对任意x1 , x2∈[0,2],当x1<x2时都有f(x1)﹣f(x2)<g(x1)﹣g(x2),则实数b的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,记f1(x)=f(f(x)),f2(x)=f(f1(x)),…,fn+1(x)=f(fn(x)),n∈N* , 那么下列说法正确的是( )
,记f1(x)=f(f(x)),f2(x)=f(f1(x)),…,fn+1(x)=f(fn(x)),n∈N* , 那么下列说法正确的是( )
A.f(x)的图象关于点(﹣1,1)对称,f2016(0)=0
B.f(x)的图象关于点(﹣1,﹣1)对称,f2016(0)=0
C.f(x)的图象关于点(﹣1,1)对称,f2016(0)=1
D.f(x)的图象关于点(﹣1,﹣1)对称,f2016(0)=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣t(t为常数)有两个零点,g(x)= ![]() .
.
(1)求g(x)的值域(用t表示);
(2)当t变化时,平行于x轴的一条直线与y=|f(x)|的图象恰有三个交点,该直线与y=g(x)的图象的交点横坐标的取值集合为M,求M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题中,正确的是( )
A.“若 ![]() ,则
,则 ![]() ”的逆命题
”的逆命题
B.命题“?x∈R, ![]() ”的否定
”的否定
C.“面积相等的三角形全等”的否命题
D.“若A∩B=B,则A?B”的逆否命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,
上一点, ![]() 为
为![]() 的中点.
的中点.
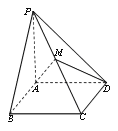
(1)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面![]() 将四棱锥
将四棱锥![]() 分成上下两部分的体积比.
分成上下两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F2(1,0),点P(1,
=1(a>b>0)的右焦点为F2(1,0),点P(1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过坐标原点O的两条直线EF,MN分别与椭圆C交于E,F,M,N四点,且直线OE,OM的斜率之积为﹣ ![]() ,求证:四边形EMFN的面积为定值.
,求证:四边形EMFN的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com