
某种产品的广告费用支出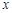 (万元)与销售额
(万元)与销售额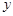 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
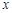 | 2 | 4 | 5 | 6 | 8 |
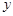 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
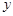 的值.
的值. ,其中
,其中 .
. 科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•福建)某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X | 1 | 2 | 3 | 4 | 5 |
| f | a | 0.2 | 0.45 | b | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率; 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小区统计部门随机抽查了区内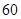 名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过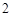 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过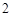 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为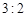 .
.
(1)确定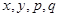 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这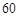 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定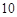 人,若需从这
人,若需从这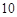 人中随机选取
人中随机选取 人进行问卷调查,设
人进行问卷调查,设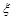 为选取的
为选取的 人中“网购红人”的人数,求
人中“网购红人”的人数,求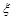 的分布列和数学期望.
的分布列和数学期望.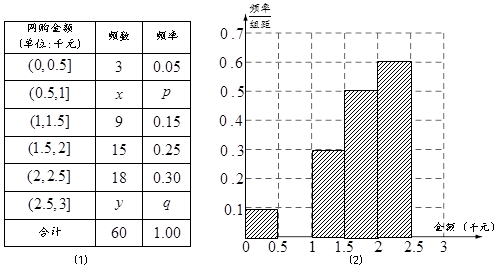
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
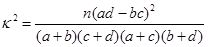
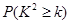 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日期 | 1月 10日 | 2月 10日 | 3月 10日 | 4月 10日 | 5月 10日 | 6月 10日 |
| 昼夜温差 x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
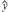 =
= x+
x+ .
. =
=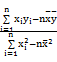 =
=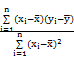 ,
, =
= -
-
 ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com