
【题目】设函数![]() ,
,![]() 已知曲线y=f(x)
已知曲线y=f(x)
在![]() 处的切线与直线
处的切线与直线![]() 垂直。
垂直。
(1) 求![]() 的值;
的值;
(2) 若对任意x≥1,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) b=1(2) (![]() ,-
,-![]() -1)∪(
-1)∪(![]() -1,1)
-1,1)
【解析】试题分析:(1)求出函数导数,由两直线垂直斜率之积为-1,解方程可得![]()
(2)求出导数,对![]() 讨论,①若
讨论,①若![]() ,则
,则![]() ;②若
;②若![]()
,则![]() ;③若
;③若![]() 三种情况分别求出单调区间,可得最小值,解不等式即可得到所求范围.
三种情况分别求出单调区间,可得最小值,解不等式即可得到所求范围.
试题解析:(1)曲线y=f(x)在点(1,f(1))处的切线斜率为2,所以f′(1)=2,又f′(x)=ln x+![]() +1,即ln 1+b+1=2,所以b=1.
+1,即ln 1+b+1=2,所以b=1.
(2) g(x)的定义域为(0,+∞),
g′(x)=![]() +(1-a)x-1=
+(1-a)x-1=![]()
![]() (x-1).
(x-1).
①若a≤![]() ,则
,则![]() ≤1,故当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上单调递增. 所以,对任意x≥1,都有g(x) >
≤1,故当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上单调递增. 所以,对任意x≥1,都有g(x) >![]() 的充要条件为g(1) >
的充要条件为g(1) >![]() ,即
,即![]() -1>
-1>![]() ,解得a<-
,解得a<-![]() -1或
-1或![]() -1 <a≤
-1 <a≤![]()
②若![]() <a<1,则
<a<1,则![]() >1,故当x∈
>1,故当x∈![]() 时,g′(x)<0;当x∈
时,g′(x)<0;当x∈![]() 时,g′(x)>0.f(x)在
时,g′(x)>0.f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以,对任意x≥1,都有g(x) >![]() 的充要条件为g
的充要条件为g![]() >
>![]() .而g
.而g![]() =aln
=aln![]() +
+![]() +
+![]() >
>![]() 在
在![]() <a<1上恒成立,
<a<1上恒成立,
所以![]() <a<1
<a<1
③若a>1,g(x)在[1,+∞)上递减,不合题意。
综上,a的取值范围是(![]() ,-
,-![]() -1)∪(
-1)∪(![]() -1,1)
-1,1)


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是矩形,侧面PAD丄底面ABCD,∠APD= ![]() . (I )求证:平面PAB丄平面PCD;
. (I )求证:平面PAB丄平面PCD;
(II)如果AB=BC,PB=PC,求二面角B﹣PC﹣D的余弦值.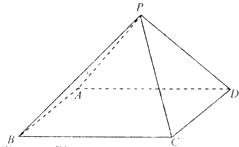
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的小球,4个不同的盒子,现要把球全部放进盒子内.
(1)恰有1个盒子不放球,共有多少种方法?
(2)恰有2个盒子不放球,共有多少种方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断居民户是否小康的一个重要指标是居民户的年收入,某市从辖区内随机抽取100个居民户,对每个居民户的年收入与年结余的情况进行分析,设第i个居民户的年收入xi(万元),年结余yi(万元),经过数据处理的: ![]() =400,
=400, ![]() =100,
=100, ![]() =900,
=900, ![]() =2850.
=2850.
(1)已知家庭的年结余y对年收入x具有线性相关关系,求线性回归方程;
(2)若该市的居民户年结余不低于5万,即称该居民户已达小康生活,请预测居民户达到小康生活的最低年收入应为多少万元? 附:在y=bx+a中,b= 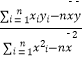 ,a=
,a= ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an+1﹣2an}是公比为2的等比数列,其中a1=1,a2=4.
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的前n项和Sn;
(3)记Cn= ![]() (n≥2),证明:
(n≥2),证明: ![]() (
( ![]() )n<
)n< ![]() +…+
+…+ ![]() ≤1﹣(
≤1﹣( ![]() )n﹣1 .
)n﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+ax﹣ ![]() 在(
在( ![]() ,+∞)是增函数,则a的取值范围( )
,+∞)是增函数,则a的取值范围( )
A.(﹣∞,3]
B.(﹣∞,﹣3]
C.[﹣3,+∞)
D.(﹣3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经研究,城市公交车的数量太多容易造成资源浪费,太少又难以满足乘客需求.为此,某市公交公司从某站占的40名候车乘客中随机抽取15人,将他们的候车时间(单位: ![]() )作为样本分成5组如下表:
)作为样本分成5组如下表:
组别 | 侯车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 2 |
四 |
| 2 |
五 |
| 3 |
(1)估计这40名乘客中侯车时间不少于20分钟的人数;
(2)若从上表侯车时间不少于10分钟的7人中选2人作进一步的问卷调查,求抽到的两人侯车时间都不少于20分钟的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com