
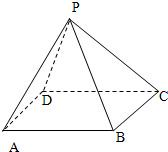
 如图,已知正四棱锥P-ABCD的底边长为6、侧棱长为5.求正四棱锥P-ABCD的体积和侧面积.
如图,已知正四棱锥P-ABCD的底边长为6、侧棱长为5.求正四棱锥P-ABCD的体积和侧面积. | 7 |
| 1 |
| 3 |
| 1 |
| 3 |
| 7 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:设计选修数学2-1苏教版 苏教版 题型:044
如图,已知正四棱锥R-ABCD的底面边长为4,高为6,点P是高的中点,点Q是侧面RBC的重心.求:
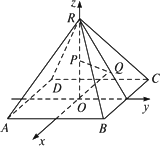
(1)异面直线PQ与BR所成的角;
(2)直线PQ与底面ABCD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
 (本小题满分13分)已知正四棱锥P—ABCD的高为
(本小题满分13分)已知正四棱锥P—ABCD的高为![]() ,底面边长为
,底面边长为![]() ,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为
,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为![]() .
.
(Ⅰ)设内接正四棱柱的体积为![]() ,求出函数
,求出函数![]() 的解析式;
的解析式;
(Ⅱ)试求该内接正四棱柱的最大体积及对应的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com