Question

【题目】某校高三年级实验班与普通班共1000名学生，其中实验班学生200人，普通班学生800人，现将高三一模考试数学成绩制成如图所示频数分布直方图，按成绩依次分为5组，其中第一组（[0， 30)），第二组（[30， 60)），第三组（[60， 90)），的频数成等比数列，第一组与第五组（[120， 150)）的频数相等，第二组与第四组（[90， 120)）的频数相等。

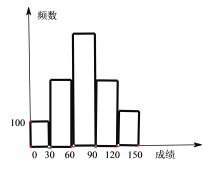
（1）求第三组的频率；

（2）已知实验班学生成绩在第五组，在第四组，剩下的都在第三组，试估计实验班学生数学成绩的平均分；

（3）在（2）的条件下，按分层抽样的方法从第5组中抽取5人进行经验交流，再从这5人中随机抽取3人在全校师生大会上作经验报告，求抽取的3人中恰有一个普通班学生的概率。

Answer 1

【答案】（1）0.4；（2）114；（3）

【解析】分析：(1)根据频率分布直方图结合等比数列的基本性质可得第三组的频率；

（2）根据题意明确各组人数，再利用平均数公式可得结果；

（3）利用古典概型概率公式即可得到抽取的3人中恰有一个普通班学生的概率.

详解：(1)设公比为，则根据题意可得 2(100＋100)＋1002＝1000，

整理得2＋2－8＝0，解得，

∴第三组的频数为 400，频率为

(2)由题意实验班学生成绩在第五组有 80 人，在第四组有 100 人，在第三组有 20 人，

∴估计平均分

(3)第 5 组中实验班与普通班的人数之比为 4∶1，∴抽取的 5 人中实验班有 4 人，普通班有 1 人，

设实验班的 4 人为 A，B，C，D，普通班 1 人为 a，则 5 人中随机抽取 3 人的结果有：ABC，ABD，ABa，ACD，ACa，ADa，BCD，BCa，BDa，CDa，共 10 种，其中恰有一个普通班学生有 6 种结果，