
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() 成立.
成立.
(1)判断f(x)在[﹣1,1]上的单调性,并证明它;
(2)解不等式f(x2)<f(2x);
(3)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】
(1)解:f(x)是[﹣1,1]上的增函数.
理由:任取x1、x2∈[﹣1,1],且x1<x2,
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)
∵ ![]() >0,
>0,
即 ![]() >0,
>0,
∵x1﹣x2<0,
∴f(x1)﹣f(x2)<0.
则f(x)是[﹣1,1]上的增函数.
(2)解:由(1)可得f(x)在[﹣1,1]递增,
可得不等式f(x2)<f(2x),即为
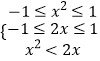 即
即 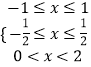
解得0<x≤ ![]() ,则解集为(0,
,则解集为(0, ![]() ];
];
(3)解:要使f(x)≤m2﹣2am+1对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,
只须f(x)max≤m2﹣2am+1,即1≤m2﹣2am+1对任意的a∈[﹣1,1]恒成立,
亦即m2﹣2am≥0对任意的a∈[﹣1,1]恒成立.令g(a)=﹣2ma+m2,
只须 ![]() ,
,
解得m≤﹣2或m≥2或m=0,
则实数m的取值范围是{m|m=0或m≤﹣2或m≥2}.
【解析】(1)利用函数单调性的定义进行证明:在区间[﹣1,1]任取x1、x2 , 且x1<x2 , 利用函数为奇函数的性质结合已知条件中的分式,可以证得f(x1)﹣f(x2)<0,所以函数f(x)是[﹣1,1]上的增函数;(2)由(1)可得f(x)在[﹣1,1]递增,不等式即为﹣1≤x2<2x≤1,解不等式即可得到所求范围;(3)根据函数f(x)≤m2﹣2am+1对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
【考点精析】通过灵活运用函数奇偶性的性质,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.


科目:高中数学 来源: 题型:
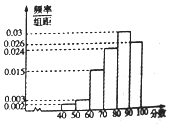
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: (I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|﹣1<x<1},B={x|2≤4x≤8},C={x|a﹣4<x≤2a﹣7}.
(1)求(UA)∩B;
(2)若A∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+ , 求g1(x),g2(x),g3(x),并猜想gn(x)的表达式(不必证明);
(2)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(3)设n∈N+ , 比较g(1)+g(2)+…+g(n)与n﹣f(n)的大小,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是R上的可导函数,对于任意的正实数t,都有函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数,则函数y=f(x)的图象可能为如图中( )
A.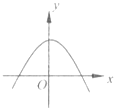
B.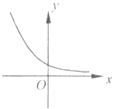
C.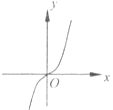
D.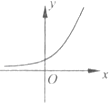
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是各项均不为0的等差数列.Sn为其前n项和,且满足an2=S2n﹣1(n∈N*),bn=an2+λan , 若{bn}为递增数列,则实数λ的范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() 的最大值为
的最大值为![]() .
.
(1)求![]() 的大小;
的大小;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图象,作出函数
的图象,作出函数![]() 在
在![]() 的图象.
的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com