
设函数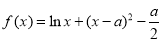 ,
,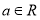 .
.
(1)若函数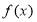 在
在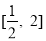 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)求函数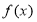 的极值点.
的极值点.
(3)设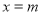 为函数
为函数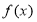 的极小值点,
的极小值点,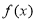 的图象与
的图象与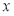 轴交于
轴交于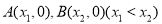 两点,且
两点,且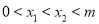 ,
,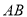 中点为
中点为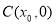 ,
,
求证: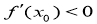 .
.
(1) ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)先求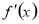 ,在
,在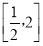 上
上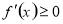 恒成立,反解参数
恒成立,反解参数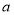 ,转化成
,转化成 恒成立问题,利用基本不等式求
恒成立问题,利用基本不等式求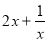 的最小值问题;
的最小值问题;
(2)先求函数的导数,因为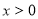 ,所以设
,所以设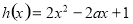 ,分情况讨论
,分情况讨论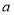 在不同情况下,
在不同情况下,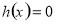 的根,通过
的根,通过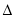 来讨论,主要分
来讨论,主要分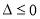 以及
以及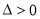 的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;
的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;
(3)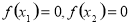 ,两式相减,结合中点坐标公式,
,两式相减,结合中点坐标公式,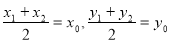 ,表示出
,表示出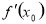 ,设出
,设出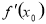 的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定
的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定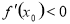 .
.
试题解析:(1)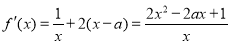
依题意得,在区间 上不等式
上不等式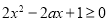 恒成立.
恒成立.
又因为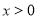 ,所以
,所以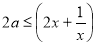 .所以
.所以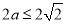 ,
,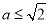
所以实数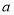 的取值范围是
的取值范围是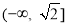 . 2分
. 2分
(2)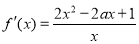 ,令
,令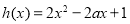
①显然,当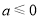 时,在
时,在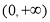 上
上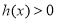 恒成立,这时
恒成立,这时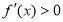 ,此时,函数
,此时,函数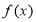 没有极值点; ..3分
没有极值点; ..3分
②当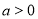 时,
时,
(ⅰ)当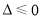 ,即
,即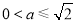 时,在
时,在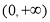 上
上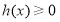 恒成立,这时
恒成立,这时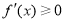 ,此时,函数
,此时,函数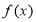 没有极值点; .4分
没有极值点; .4分
(ⅱ)当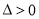 ,即
,即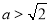 时,
时,
易知,当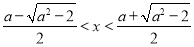 时,
时,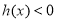 ,这时
,这时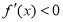 ;
;
当 或
或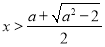 时,
时,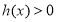 ,这时
,这时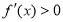 ;
;
所以,当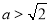 时,
时,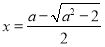 是函数
是函数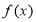 的极大值点;
的极大值点;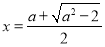 是函数
是函数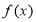 的极小值点.
的极小值点.
综上,当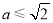 时,函数
时,函数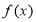 没有极值点; .6分
没有极值点; .6分
当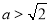 时,
时,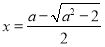 是函数
是函数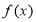 的极大值点;
的极大值点;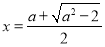 是函数
是函数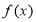 的极小值点. 8分
的极小值点. 8分
(Ⅲ)由已知得 两式相减,
两式相减,
得: ①
①
由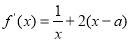 ,得
,得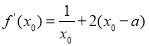 ②得①代入②,得
②得①代入②,得
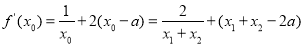
= 10分
10分
令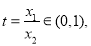 且
且
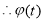 在
在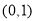 上递减,
上递减,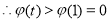
 12分
12分
考点:导数的综合性问题


科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:选择题
二项式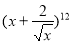 展开式中的常数项是( )
展开式中的常数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
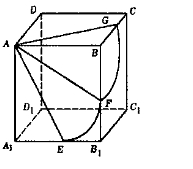
如图,正方体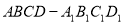 的棱长为
的棱长为 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
A.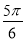 B.
B.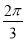 C.
C.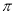 D.
D.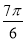
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试理科数学试卷(解析版) 题型:选择题
个棱锥的三视图如上图,则该棱锥的全面积(单位:cm2)为( )
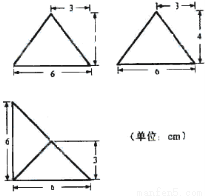
A.48+12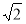 B.48+24
B.48+24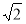 C.36+12
C.36+12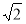 D.36+24
D.36+24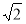
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
如图,在长方体 中,
中,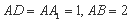 .
.
(1)若点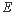 在对角线
在对角线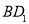 上移动,求证:
上移动,求证: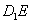 ⊥
⊥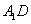 ;
;
(2)当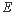 为棱
为棱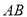 中点时,求点
中点时,求点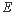 到平面
到平面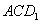 的距离。
的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com