
【题目】已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,且过点
倍,且过点![]() .
.
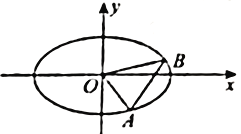
(1)求椭圆的标准方程;
(2)若![]() 的顶点
的顶点![]() 、
、![]() 在椭圆上,
在椭圆上, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,
, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】试题分析:(1)根据椭圆长轴与短轴的关系列出一个方程,再根据椭圆过已知点列出一个方程,解方程组求出a,b,写出椭圆的标准方程;(2)由于OA和OB的斜率乘积为定值,因此OA的斜率为![]() ,则OB的斜率可表示为
,则OB的斜率可表示为![]() ,分别把射线OA、OB的方程与椭圆的方程联立,求出A、B两点的横坐标,得出两点的横坐标的积,根据OA、OB方程得出A、B两点的纵坐标的积,从表示出数量积
,分别把射线OA、OB的方程与椭圆的方程联立,求出A、B两点的横坐标,得出两点的横坐标的积,根据OA、OB方程得出A、B两点的纵坐标的积,从表示出数量积![]() ,再利用基本不等式求出最值.
,再利用基本不等式求出最值.
试题解析:
(1)由题意得 解得
解得
∴椭圆的标准方程为![]() .
.
(2)设![]() ,
, ![]() ,不妨设
,不妨设![]() ,
, ![]() .
.
由![]() ,∴
,∴![]() (
(![]() ),
),
直线![]() 、
、![]() 的方程分别为
的方程分别为![]() ,
, ![]() ,
,
联立
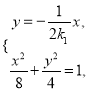
解得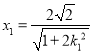 ,
, 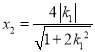 .
.
∵![]()
 ,
,
当且仅当![]() 时,等号成立.
时,等号成立.
所以![]() 的最大值为2.
的最大值为2.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的有( )
①随机事件A的概率是频率的稳定值,频率是概率的近似值.
②一次试验中不同的基本事件不可能同时发生.
③任意事件A发生的概率![]() 总满足
总满足![]() .
.
④若事件A的概率为0,则A是不可能事件.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为
的距离为![]() ,以
,以![]() 为圆心且与抛物线准线
为圆心且与抛物线准线![]() 相切的圆恰好过原点
相切的圆恰好过原点![]() .点
.点![]() 是
是![]() 与
与![]() 轴的交点,
轴的交点, ![]() 两点在抛物线上且直线
两点在抛物线上且直线![]() 过
过![]() 点,过
点,过![]() 点及
点及![]() 的直线交抛物线于
的直线交抛物线于![]() 点.
点.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:直线![]() 过一定点,并求出该点坐标.
过一定点,并求出该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在元旦期间开展优惠酬宾活动,凡购物满100元可抽奖一次,满200元可抽奖两次…依此类推.抽奖箱中有7个白球和3个红球,其中3个红球上分别标有10元,10元,20元字样.每次抽奖要从抽奖箱中有放回地任摸一个球,若摸到红球,根据球上标注金额奖励现金;若摸到白球,没有任何奖励.
(Ⅰ)一次抽奖中,已知摸中了红球,求获得20元奖励的概率;
(Ⅱ)小明有两次抽奖机会,用![]() 表示他两次抽奖获得的现金总额,写出
表示他两次抽奖获得的现金总额,写出![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的公比
的公比![]() ,前n项和为
,前n项和为![]() .若
.若![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的前2019项和;
的前2019项和;
(3)设![]() ,问数列
,问数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com