
����Ŀ��ijѧУ��һ ���߶� �����������꼶���� ![]() ����ʦ��Ϊ�������ǵı���ʱ�������ͨ���ֲ�
����ʦ��Ϊ�������ǵı���ʱ�������ͨ���ֲ�
���������![]() ����ʦһ�ܵı���ʱ�� ���������±�����λ ��Сʱ����
����ʦһ�ܵı���ʱ�� ���������±�����λ ��Сʱ����
��һ�꼶 |
|
|
|
|
| |||
�߶��꼶 |
|
|
|
|
|
|
| |
�����꼶 |
|
|
|
|
|
|
|
|
��1���Թ��Ƹ�У�����꼶�Ľ�ʦ���� ��
��2���Ӹ�һ�꼶�߶��꼶����Ľ�ʦ�У������ѡȡһ�ˣ���һ�꼶ѡ�����˼�Ϊ�� ���߶��꼶ѡ�����˼�Ϊ�� ������ܼı���ʱ�䲻���ҵı���ʱ�䳤�ĸ��� ��
��3���ٴӸ�һ���߶������������꼶�и������ȡһ����ʦ�����Ǹ��ܵı���ʱ��ֱ���![]() ����λ�� Сʱ��������������������е����ݹ��ɵ���������ƽ������Ϊ
����λ�� Сʱ��������������������е����ݹ��ɵ���������ƽ������Ϊ![]() �������е�����ƽ������Ϊ
�������е�����ƽ������Ϊ![]() �����ж�
�����ж�![]() ��
��![]() �Ĵ�С. �����۲�Ҫ��֤����
�Ĵ�С. �����۲�Ҫ��֤����
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
�������������������1��ֱ�Ӹ��ݷֲ�����������ɵø����꼶�Ľ�ʦ����![]() ���ˣ�����2�����ݻ����¼��������¼��ĸ��ʹ�ʽ��⣻��3���ֱ����������ƽ��ֵ
���ˣ�����2�����ݻ����¼��������¼��ĸ��ʹ�ʽ��⣻��3���ֱ����������ƽ��ֵ![]() ���Լ��¼����������
���Լ��¼����������![]() ��ƽ����Ϊ9���Ƚϴ�С����.
��ƽ����Ϊ9���Ƚϴ�С����.
�����������1�������20λ��ʦ�У����Ը����꼶����8����
���ݷֲ���������������꼶�Ľ�ʦ����![]() ���ˣ�
���ˣ�
��2�����¼�Ϊ![]() ���������������и�һ�꼶�еĵ�
���������������и�һ�꼶�еĵ�![]() ����ʦ����
����ʦ���� ![]() ��
��
�¼�![]() ���������������и߶��꼶�еĵ�
���������������и߶��꼶�еĵ�![]() ����ʦ����
����ʦ���� ![]() ��
��
������֪�� ![]() ��
�� ![]() ��
��
![]()
���¼�![]() Ϊ�����ܼı���ʱ����ҵı���ʱ�䳤����������֪��
Ϊ�����ܼı���ʱ����ҵı���ʱ�䳤����������֪��
![]()
����![]()
![]()
��![]() ��
��
��3��![]() ��
�� ![]() ��
��
![]()
������ƽ��ֵ![]() ��
��
�¼����������![]() ��ƽ����Ϊ9����
��ƽ����Ϊ9����![]() С��
��
��������ƽ��ֵ����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �Ľ�����
�Ľ�����![]() ���ϣ�����Բ
���ϣ�����Բ![]() �Ľ���Ϊ2��
�Ľ���Ϊ2��
��������Բ![]() �ı����̣�
�ı����̣�
������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��������
��������![]() ����
����![]() ��
��![]() ��������Բ
��������Բ![]() ������һ��
������һ��![]() ��
�� ![]() Ϊ��Բ
Ϊ��Բ![]() ���ҽ��㣬��֤������
���ҽ��㣬��֤������![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���acos2 ![]() +ccos2
+ccos2 ![]() =
= ![]() b����ôa��b��c�Ĺ�ϵ�ǣ� ��
b����ôa��b��c�Ĺ�ϵ�ǣ� ��
A.a+b=c
B.a+c=2b
C.b+c=2a
D.a=b=c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ݵ�ƽ������2.8��������3.6���������������е�ÿһ�����ݶ�����60���õ�һ�������ݣ������������ݵ�ƽ�����ͷ���ֱ��ǣ� ��
A.57.2��3.6
B.57.2��56.4
C.62.8��63.6
D.62.8��3.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ǹ��������ȵ����У�
�Ǹ��������ȵ����У� ![]() Ϊ����ǰ
Ϊ����ǰ![]() ��ͣ�����
��ͣ�����![]() .
.
��1����![]() ����
����![]() �ɵȲ����У���
�ɵȲ����У���![]() ��ֵ��
��ֵ��
��2����![]() �ĸ��������ȣ��ʵ��ҽ���
�ĸ��������ȣ��ʵ��ҽ���![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]() �ɵȲ����У���˵������.
�ɵȲ����У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ְԺУ�������������Ļ����ʿ��ԣ���������Ϊ���ġ���ѧ��Ӣ�����ƣ��ܷ�Ϊ200��.�ִ����ߵĿ����������ȡ20�ˣ�����ɼ��þ�Ҷͼ��¼���£�
�� | ٠| |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
���������߿����г�ȡ�������ɼ��ķ���![]() ���������ȷ��С�����һλ��
���������ȷ��С�����һλ��
����������Ҷͼ180�����ϵĿ�������ѡ2����Ϊ����������ϯ��̸�ᣬ����ѡ����ǡΪһ��һŮ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���Sn=3n2+8n��{bn}�ǵȲ����У���an=bn+bn+1 ��
����������{bn}��ͨ�ʽ��
������cn= ![]() ��������{cn}��ǰn���Tn ��
��������{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD�������Σ�����PD�͵���ABCD��PD=DC��E��PC���е㣬��EF��PB��PB�ڵ�F�� 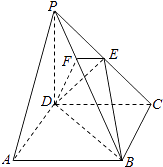
��1��֤��PA��ƽ��EDB��
��2��֤��PB��ƽ��EFD��
��3��������C��PB��D�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2px����P��1��1��.���㣨0��![]() ����ֱ��l��������C���ڲ�ͬ������M��N������M��x��Ĵ��߷ֱ���ֱ��OP��ON���ڵ�A��B������OΪԭ��.
����ֱ��l��������C���ڲ�ͬ������M��N������M��x��Ĵ��߷ֱ���ֱ��OP��ON���ڵ�A��B������OΪԭ��.
��������������C�ķ��̣������佹��������߷��̣�
��������֤��AΪ�߶�BM���е�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com