
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,a2+b2+c2=ac+bc+ca.
(1)证明:△ABC是正三角形;
(2)如图,点D的边BC的延长线上,且BC=2CD,AD= ![]() ,求sin∠BAD的值.
,求sin∠BAD的值. 
【答案】
(1)证明:由a2+b2+c2=ac+bc+ca,
得(a﹣b)2+(b﹣c)2+(c﹣a)2=0,
所以a﹣b=b﹣c=c﹣a=0,
所以a=b=c,
即△ABC是正三角形
(2)解:因为△ABC是等边三角形,BC=2CD,
所以AC=2CD,∠ACD=120°,
所以在△ACD中,由余弦定理可得:AD2=AC2+CD2﹣2ACCDcos∠ACD,
可得:7=4CD2+CD2﹣4CDCDcos120°,解得CD=1,
在△ABC中,BD=3CD=3,由正弦定理可得sin∠BAD= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由已知利用配方法可得(a﹣b)2+(b﹣c)2+(c﹣a)2=0,从而可求a=b=c,即△ABC是正三角形.(2)由已知可求AC=2CD,∠ACD=120°,由余弦定理可解得CD=1,又BD=3CD=3,由正弦定理可得sin∠BAD= ![]() 的值.
的值.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】点S、A、B、C在半径为 ![]() 的同一球面上,点S到平面ABC的距离为
的同一球面上,点S到平面ABC的距离为 ![]() ,AB=BC=CA=
,AB=BC=CA= ![]() ,则点S与△ABC中心的距离为( )
,则点S与△ABC中心的距离为( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2,直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.点M为线段BC的中点,点P是线段BB1中点. (Ⅰ)求证:A1C1⊥AP;
(Ⅱ)求二面角P﹣AM﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖. (Ⅰ)求分别获得一、二、三等奖的概率;
(Ⅱ)设摸球次数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的方程为y= ![]() x,曲线C的参数方程为
x,曲线C的参数方程为 ![]() (φ是参数,0≤φ≤π).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ是参数,0≤φ≤π).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)分别写出直线l1与曲线C的极坐标方程;
(2)若直线 ![]() =0,直线l1与曲线C的交点为A,直线l1与l2的交点为B,求|AB|.
=0,直线l1与曲线C的交点为A,直线l1与l2的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=3,AA1=3 ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . (Ⅰ)证明:BC⊥AB1;
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . (Ⅰ)证明:BC⊥AB1;
(Ⅱ)若OC=OA,求二面角A1﹣AC﹣B的余弦值.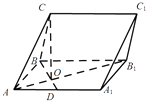
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 f (x)=|x﹣1|+|x﹣a|(a∈R).
(1)若a=﹣3,求函数 f (x)的最小值;
(2)如果x∈R,f (x)≤2a+2|x﹣1|,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com