练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的22列联表：

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由算得，.

    附表：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是（ ）

    A.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”；

    B.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”；

    C.有99%以上的把握认为“爱好该项运动与性别有关”；

    D.有99%以上的把握认为“爱好该项运动与性别无关”．

    【答案】C

    【解析】

    根据给定的的值，结合附表，即可得到结论.

    由 ，

    所以有99%以上的把握认为“爱好该项运动与性别有关.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列三个命题：

    ①函数的单调增区间是

    ②经过任意两点的直线，都可以用方程来表示；

    ③命题：“ ，”的否定是“，”，

    其中正确命题的个数有（ ）个

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2012年的自主招生考试成绩中随机抽取名中学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．

    组号

    分组

    频数

    频率

    第1组

    5

    第2组

    ①

    第3组

    30

    ②

    第4组

    20

    第5组

    10

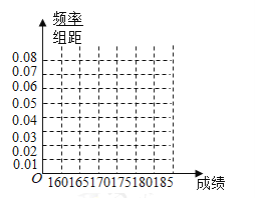
    （1）请先求出频率分布表中位置的相应数据，再完成频率分布直方图；

    （2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第组中用分层抽样抽取名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试；

    （3）在（2）的前提下，学校决定在名学生中随机抽取名学生接受考官进行面试，求：第组至少有一名学生被考官面试的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若“，使得”为真命题，求的取值范围；

    （2）若不等式的解集为D，若，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）g（x）分别是定义在R上的偶函数和奇函数，且f（x）+g（x）=23x．

    （1）证明：f（x）-g（x）=23-x，并求函数f（x），g（x）的解析式；

    （2）解关于x不等式：g（x2+2x）+g（x-4）＞0；

    （3）若对任意x∈R，不等式f（2x）≥mf（x）-4恒成立，求实数m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AB//CD，且

    （1）证明：平面PAB⊥平面PAD；

    （2）若PA=PD=AB=DC, ,且四棱锥P-ABCD的体积为，求该四棱锥的侧面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费支出x（单位：百万元）与销售额y（单位：百万元）之间有如下的对应数据：

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

    （1）画出散点图；

    （2）求y关于x的线性回归方程.

    （3）如果广告费支出为一千万元，预测销售额大约为多少百万元？

    参考公式用最小二乘法求线性回归方程系数公式：，.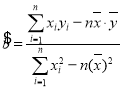

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对下列命题：

    ①直线与函数的图象相交，则相邻两交点的距离为；

    ②点 是函数的图象的一个对称中心；

    ③函数在上单调递减，则的取值范围为；

    ④函数若对R恒成立，则.

    其中所有正确命题的序号为____

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）（k＞0）

    （1）若f（x）＞m的解集为{x|x＜-3，或x＞-2}，求不等式5mx2+kx+3＞0的解集；

    （2）若存在x＞3，使得f（x）＞1成立，求k的取值范围．

    查看答案和解析>>

    同步练习册答案