
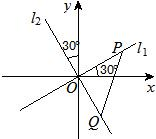
 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,已知线段PQ的长度为2,且点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动.| x12 |
| 3 |
| OA |
| OB |
 解:(Ⅰ)由已知得直线l1⊥l2,l1:y=
解:(Ⅰ)由已知得直线l1⊥l2,l1:y=
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 4 |
| 3 |
| x12 |
| 3 |
| x2 |
| 3 |
| x2 |
| 3 |
| 12kx |
| 1+3k2 |
| 9 |
| 1+3k2 |
| OA |
| OB |
| 12kx |
| 1+3k2 |
| 9 |
| 1+3k2 |
| 13-3k2 |
| 1+3k2 |
| 13 |
| 3 |
| 13 |
| 3 |
| ||
| 3 |
| ||
| 3 |


科目:高中数学 来源:2010-2011学年湖南省株洲二中高三(下)第十次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年福建省泉州五中高考数学模拟试卷1(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市第二高级中学高考数学模拟试卷2(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2009年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com