
【题目】对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:
1)f(x)在[m,n]上是单调的;
2)当定义域是[m,n]时,f(x)的值域也是[m,n],则称[m,n]是该函数的“和谐区间”.若函数f(x)= ![]() ﹣
﹣ ![]() (a>0)存在“和谐区间”,则实数a的取值范围是 .
(a>0)存在“和谐区间”,则实数a的取值范围是 .
【答案】0<a<1
【解析】解:由题意可得函数 ![]() 在区间[m,n]是单调递增的,
在区间[m,n]是单调递增的,
∴[m,n](﹣∞,0)或[m,n](0,+∞),则f(m)=m,f(n)=n,
故m、n是方程f(x)=x的两个同号的不等实数根,
即 ![]() ,
,
即方程ax2﹣(a+1)x+a=0有两个同号的实数根,
∵mn= ![]() ,
,
故只需△=(a+1)2﹣4a2>0,解得 ![]() <a<1,
<a<1,
∵a>0,
∴0<a<1.
所以答案是:0<a<1.
【考点精析】通过灵活运用函数的值域和函数单调性的判断方法,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较即可以解答此题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)若直线![]() 过焦点
过焦点![]() ,且与圆
,且与圆![]() 交于
交于![]() (其中
(其中![]() 在
在![]() 轴同侧),求证:
轴同侧),求证: ![]() 是定值;
是定值;
(Ⅱ)设抛物线![]() 在
在![]() 和
和![]() 点的切线交于点
点的切线交于点![]() ,试问:
,试问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为菱形?若存在,请说明理由并求此时直线
为菱形?若存在,请说明理由并求此时直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出的样本频率分布直方图如图,那么在这片树木中底部周长大于100cm的株树大约中( ) 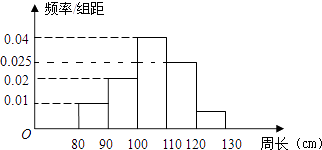
A.3000
B.6000
C.7000
D.8000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C,坐标原点为O.
,连接PA交椭圆于点C,坐标原点为O.
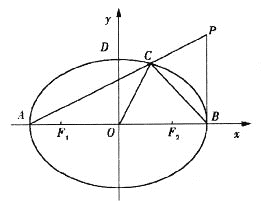
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2],上是减函数,且对任意的x1 , x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 和
和![]() ,若存在常数
,若存在常数![]() ,对于任意
,对于任意![]() ,不等式
,不等式![]() 都成立,则称直线
都成立,则称直线![]() 是函数
是函数![]() 的分界线. 已知函数
的分界线. 已知函数![]() 为自然对数的底,
为自然对数的底, ![]() 为常数
为常数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,试探究函数
,试探究函数![]() 与函数
与函数![]() 是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com