
【题目】为了加强中学生实践、创新和团队建设能力的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(1)完成频率分布表(直接写出结果);
(2)若成绩在90.5分以上的学生获一等奖,试估计全校获一等奖的人数,现在从全校所有获一等奖的同学中随机抽取2名同学代表学校参加竞赛,某班共有2名同学荣获一等奖,求该班同学恰有1人参加竞赛的概率.
分组 | 频数 | 频率 | |
第1组 | [60.5,70.5) | 0.26 | |
第2组 | [70.5,80.5) | 17 | |
第3组 | [80.5,90.5) | 18 | 0.36 |
第4组 | [90.5,100.5] | ||
合计 | 50 | 1 |
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据频率、频数与总数关系分别计算并填表,(2)先根据频率、频数与总数关系估计全校获一等奖的人数,再利用枚举法得总事件数以及所求事件包含事件数,最后根据古典概型概率公式求结果.
(1)作出频率分布表如下:
频数 | 频率 | |
第1组 | 13 | 0.26 |
第2组 | 17 | 0.34 |
第3组 | 18 | 0.36 |
第4组 | 2 | 0.04 |
合计 | 50 | 1 |
(2)获得一等奖的概率约为0.04,
∴获得一等奖的人数估计为150×0.04=6(人),其中,该班共有2名同学荣获一等奖,
记获得一等奖的这6人为: A1,A2,B,C,D,E,共中A1,A2为该班获得一等奖的同学,
从全校所有获得一等奖的6名同学中抽取2名同学代表全校参加竞赛共有(A1,B),(A1,C),(A1,D),(A1,E),(A2,B),(A2,C),(A2,D),(A2,E),(A1,A2),(B,C),(B,D),(B,E),(C,D),(C,E),(E,D)共![]() 种情况,该班同学恰恰有1人参加竞赛的情况有8种,分别为:(A1,B),(A1,C),(A1,D),(A1,E),(A2,B),(A2,C),(A2,D),(A2,E),∴该班同学恰有1人参加竞赛的概率P=
种情况,该班同学恰恰有1人参加竞赛的情况有8种,分别为:(A1,B),(A1,C),(A1,D),(A1,E),(A2,B),(A2,C),(A2,D),(A2,E),∴该班同学恰有1人参加竞赛的概率P=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设命题p:方程x2+(2m-4)x+m=0有两个不等的实数根:命题q:x∈[2,3],不等式x2-4x+13≥m2恒成立.
(1)若命题p为真命题,则实数m的取值范围;
(2)若命题p∨q为真命题,命题p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
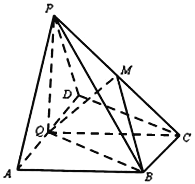
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.
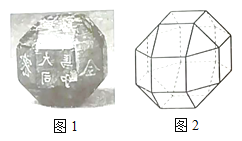
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列判断正确的是()
对称,则下列判断正确的是()
A. 函数![]() 在
在![]() 上单调递增
上单调递增
B. 函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
C. 当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
D. 要得到函数![]() 的图像,只需要
的图像,只需要![]() 将的图像向右平移
将的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织高一年级学生到古都西安游学.在某景区,由于时间关系,每个班只能在甲、乙、丙三个景点中选择一个游览.高一![]() 班的
班的![]() 名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有
名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有![]() 人会选择甲,在乙、丙两个景点中有
人会选择甲,在乙、丙两个景点中有![]() 人会选择乙.那么关于这轮投票结果,下列说法正确的是
人会选择乙.那么关于这轮投票结果,下列说法正确的是
①该班选择去甲景点游览;
②乙景点的得票数可能会超过![]() ;
;
③丙景点的得票数不会比甲景点高;
④三个景点的得票数可能会相等.
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0.
(1)求数列的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com