
【题目】若对任意的正整数![]() ,集合
,集合![]() 的任意
的任意![]() 元子集中,总有三个元素两两互素.求
元子集中,总有三个元素两两互素.求![]() 的最小值.
的最小值.
【答案】68
【解析】
考虑![]() 时的集合
时的集合![]() 的67元子集,其元素为偶数及被3整除的奇数,即
的67元子集,其元素为偶数及被3整除的奇数,即
![]() .
.
显然,集合![]() 中不存在三个两两互素的元素.
中不存在三个两两互素的元素.
于是,![]() 不符合要求.
不符合要求.
下面证明![]() 符合要求.
符合要求.
先证明一个引理.
引理对任意的正整数![]() ,集合
,集合
![]() 的任意五元子集中,总有三个元素两两互素.
的任意五元子集中,总有三个元素两两互素.
证明,设![]() 为集合
为集合![]() 的一个五元子集.
的一个五元子集.
注意到,![]() 这六个数三奇三偶,且恰有一个为5的倍数.
这六个数三奇三偶,且恰有一个为5的倍数.
于是,若集合![]() 中含有三个奇数,则这三个奇数必两两互素,结论成立.
中含有三个奇数,则这三个奇数必两两互素,结论成立.
若集合![]() 中元素为两奇三偶,由于三个偶数中至多有一个为3的倍数,至多有一个为5的倍数,因此,三个偶数中必有一个数既不为3的倍数,也不为5的倍数,它与两个奇数两两互素,结论成立.
中元素为两奇三偶,由于三个偶数中至多有一个为3的倍数,至多有一个为5的倍数,因此,三个偶数中必有一个数既不为3的倍数,也不为5的倍数,它与两个奇数两两互素,结论成立.
回到原题.
对任意的正整数![]() ,将集合
,将集合![]() 划分成如下17个集合:
划分成如下17个集合:
![]() ,
,
![]() ,
,
设![]() 为集合
为集合![]() 的68元子集.
的68元子集.
(1)若集合![]() 有四个元素来自集合
有四个元素来自集合![]() ,由于
,由于![]() 为奇数时,
为奇数时,![]() 、
、![]() 、
、![]() 两两互素;
两两互素;![]() 为偶数时,
为偶数时,![]() 、
、![]() 、
、![]() 两两互素,因此,集合
两两互素,因此,集合![]() 中至少有三个元素两两互素.
中至少有三个元素两两互素.
(2)若集合![]() 至多有三个元素来自集合
至多有三个元素来自集合![]() ,则集合
,则集合![]() 至少有65个元素来自集合
至少有65个元素来自集合![]() .
.
根据抽屉原理,知集合![]() 至少有五个元素来自同一个集合,不妨设其来自集合
至少有五个元素来自同一个集合,不妨设其来自集合![]() .由引理,知它们中存在三个两两互素的元素.因此,集合
.由引理,知它们中存在三个两两互素的元素.因此,集合![]() 中总有三个两两互素的元素.
中总有三个两两互素的元素.
从而,![]() 符合要求,即对任意的正整数
符合要求,即对任意的正整数![]() ,集合
,集合![]() 的任意68元子集中,总有三个元素两两互素.
的任意68元子集中,总有三个元素两两互素.
综上,![]() 的最小值为68.
的最小值为68.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足![]() ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水![]() 米到水底进行考古作业,其用氧量包含以下三个方面:
米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升.
米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(Ⅰ)如果水底作业时间是![]() 分钟,将
分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
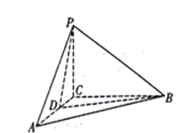
(1)证明:PC⊥平面ABC;
(2)若点D在棱AC上,且二面角D-PB-C为30°,求PD与平面PAB所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将四边形
的中点,将四边形![]() 沿直线
沿直线![]() 进行翻折,给出下列四个结论:①
进行翻折,给出下列四个结论:①![]() ;②
;②![]() ③平面
③平面![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() ,则上述结论可能正确的是( ).
,则上述结论可能正确的是( ).
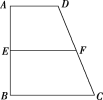
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
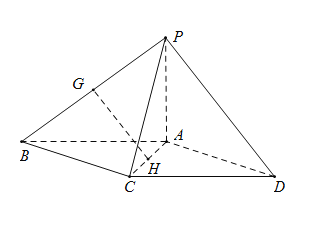
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列
的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列![]() 的前n项和Sn=f(n)(n∈N*).
的前n项和Sn=f(n)(n∈N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列{![]() }前n项的和Tn.
}前n项的和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com