
【题目】已知椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
,F1 , F2分别是它的左、右焦点,且存在直线l,使F1 , F2关于l的对称点恰好为圆C:x2+y2﹣4mx﹣2my+5m2﹣4=0(m∈R,m≠0)的一条直径的两个端点.
(1)求椭圆E的方程;
(2)设直线l与抛物线y2=2px(p>0)相交于A,B两点,射线F1A,F1B与椭圆E分别相交于点M,N,试探究:是否存在数集D,当且仅当p∈D时,总存在m,使点F1在以线段MN为直径的圆内?若存在,求出数集D;若不存在,请说明理由.
【答案】
(1)解:将圆C的方程配方的:(x﹣2m)2+(y﹣m)2=4,则圆心C(2m,m),半径为2,
由椭圆的焦距为2c=d=4,c=2,
由e= ![]() =
= ![]() ,则a=3,
,则a=3,
b2=a2﹣c2=5,故椭圆的方程为 ![]() ;
;
(2)由F1,F2关于l的对称点恰好是圆C的一条直径的两个端点,则直线l是线段OC的垂直平分线,
故l方程为y=﹣2x+ ![]() ,
,
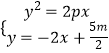 ,整理得2y2+2py﹣5pm=0,
,整理得2y2+2py﹣5pm=0,
则△=(2p)2+4×2×5p>0,则p+10m>0,
设A(x1,y1),B(x1,y1),则y1+y2=﹣p,y1y1=﹣ ![]() ,
,
由F1的坐标为(﹣2,0),则 ![]() =(x1+2,y1),
=(x1+2,y1), ![]() =(x2+2,y2),
=(x2+2,y2),
由 ![]() 与
与 ![]() 同向,
同向, ![]() 与
与 ![]() 同向,
同向,
则点F1在以线段MN为直径的圆内,则 ![]()
![]() <0,则
<0,则 ![]()
![]() <0,
<0,
则(x1+2)(x2+2)+y1y2<0,即x1x2+2(x1+x2)+4+y1y1<0,则 ![]() +10(2﹣p)m+4(p+4)<0,
+10(2﹣p)m+4(p+4)<0,
当且仅当△=100(2﹣p)2﹣100(p+4)>0,即p>5,
总存在m使得②成立,
当p>5时,由韦达定理可知 ![]() +10(2﹣p)m+4(p+4)=0的两个根为正数,
+10(2﹣p)m+4(p+4)=0的两个根为正数,
故使②成立的m>0,从而满足①,
故存在整数集D=(5,+∞),当且仅当p∈D时,总存在m,使点F1在线段MN为直径的圆内.
【解析】(1)将圆C的一般方程变为标准方程,得到圆心坐标和半径,根据题意不难得到椭圆方程中的a,b,c,(2)由F1,F2关于l的对称点恰好是圆C的一条直径的两个端点,则直线l是线段OC的垂直平分线,可得到直线l的方程,联立抛物线方程,由韦达定理得到y1+y2,y1y1,根据点 F1在以线段MN为直径的圆内,可得到 ![]()
![]() <0,表示出向量进行求解即可.
<0,表示出向量进行求解即可.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)已知 ![]() ,其中ai∈R,i=1,2,…10.
,其中ai∈R,i=1,2,…10.
(i)求a0+a1+a2+…+a10;
(ii)求a7 .
(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至少有一人参加,且五人均能胜任这四个岗位.
(i)若每人不准兼职,则不同的分配方案有几种?
(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案有几种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 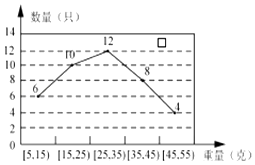
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是双曲线
是双曲线 ![]() 的右焦点,过点
的右焦点,过点 ![]() 作
作 ![]() 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ![]() ,线段
,线段 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,记点
,记点 ![]() 到
到 ![]() 的两条渐近线的距离之积为
的两条渐近线的距离之积为 ![]() ,若
,若 ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.![]()
B.2
C. 3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() +cx+d有极值.
+cx+d有极值.
(Ⅰ)求实数c的取值范围;
(Ⅱ)若f(x)在x=2处取得极值,且当x<0时,f(x)< ![]() +2d恒成立,求实数d的取值范围.
+2d恒成立,求实数d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx﹣cos2x﹣
sinxcosx﹣cos2x﹣ ![]() .
.
(Ⅰ)求函数f(x)的对称轴方程;
(Ⅱ)将函数f(x)的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移 ![]() 个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
个单位,得到函数g(x)的图象.若a,b,c分别是△ABC三个内角A,B,C的对边,a=2,c=4,且g(B)=0,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1 , a3 , a7成等比数列,且a2n=2an﹣1,等比数列{bn}满足bn+bn+1= ![]() .
.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com